Logarithmic landscape and power-law escape rate of SGD

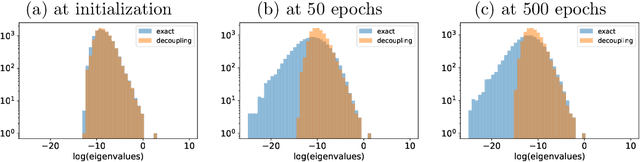
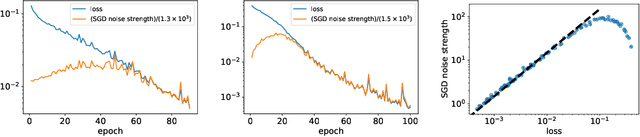
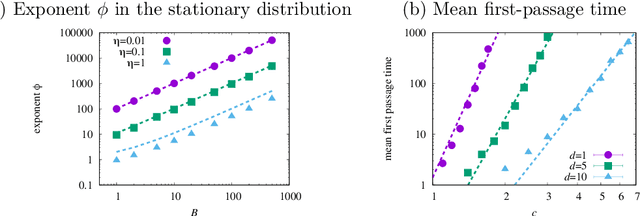
Stochastic gradient descent (SGD) undergoes complicated multiplicative noise for the mean-square loss. We use this property of the SGD noise to derive a stochastic differential equation (SDE) with simpler additive noise by performing a non-uniform transformation of the time variable. In the SDE, the gradient of the loss is replaced by that of the logarithmized loss. Consequently, we show that, near a local or global minimum, the stationary distribution $P_\mathrm{ss}(\theta)$ of the network parameters $\theta$ follows a power-law with respect to the loss function $L(\theta)$, i.e. $P_\mathrm{ss}(\theta)\propto L(\theta)^{-\phi}$ with the exponent $\phi$ specified by the mini-batch size, the learning rate, and the Hessian at the minimum. We obtain the escape rate formula from a local minimum, which is determined not by the loss barrier height $\Delta L=L(\theta^s)-L(\theta^*)$ between a minimum $\theta^*$ and a saddle $\theta^s$ but by the logarithmized loss barrier height $\Delta\log L=\log[L(\theta^s)/L(\theta^*)]$. Our escape-rate formula explains an empirical fact that SGD prefers flat minima with low effective dimensions.

On Minibatch Noise: Discrete-Time SGD, Overparametrization, and Bayes

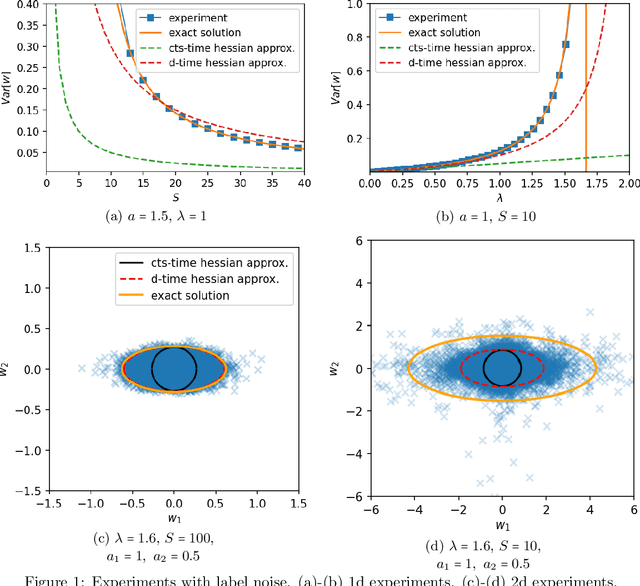
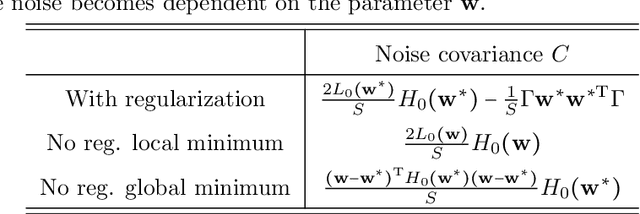
The noise in stochastic gradient descent (SGD), caused by minibatch sampling, remains poorly understood despite its enormous practical importance in offering good training efficiency and generalization ability. In this work, we study the minibatch noise in SGD. Motivated by the observation that minibatch sampling does not always cause a fluctuation, we set out to find the conditions that cause minibatch noise to emerge. We first derive the analytically solvable results for linear regression under various settings, which are compared to the commonly used approximations that are used to understand SGD noise. We show that some degree of mismatch between model and data complexity is needed in order for SGD to "cause" a noise, and that such mismatch may be due to the existence of static noise in the labels, in the input, the use of regularization, or underparametrization. Our results motivate a more accurate general formulation to describe minibatch noise.

Stochastic Gradient Descent with Large Learning Rate

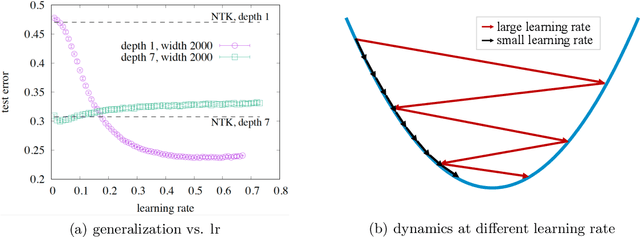
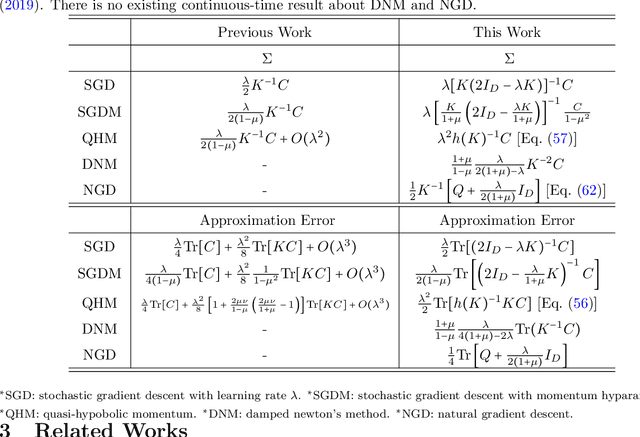
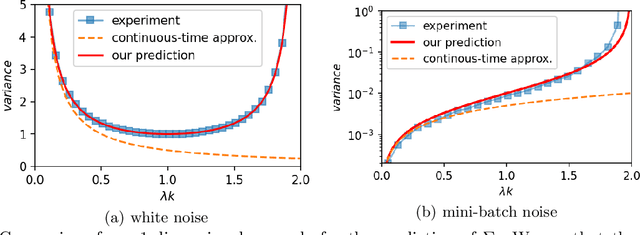
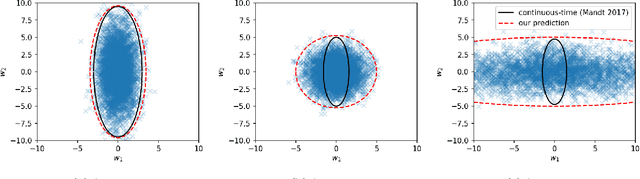
As a simple and efficient optimization method in deep learning, stochastic gradient descent (SGD) has attracted tremendous attention. In the vanishing learning rate regime, SGD is now relatively well understood, and the majority of theoretical approaches to SGD set their assumptions in the continuous-time limit. However, the continuous-time predictions are unlikely to reflect the experimental observations well because the practice often runs in the large learning rate regime, where the training is faster and the generalization of models are often better. In this paper, we propose to study the basic properties of SGD and its variants in the non-vanishing learning rate regime. The focus is on deriving exactly solvable results and relating them to experimental observations. The main contributions of this work are to derive the stable distribution for discrete-time SGD in a quadratic loss function with and without momentum. Examples of applications of the proposed theory considered in this work include the approximation error of variants of SGD, the effect of mini-batch noise, the escape rate from a sharp minimum, and and the stationary distribution of a few second order methods.