Logarithmic landscape and power-law escape rate of SGD
Paper and Code
May 20, 2021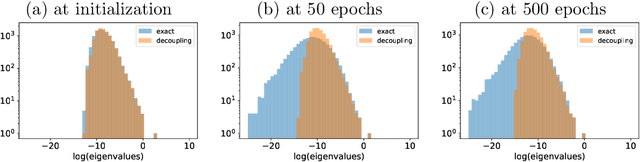
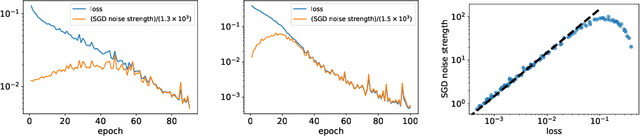
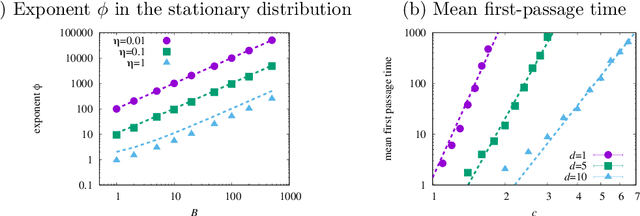
Stochastic gradient descent (SGD) undergoes complicated multiplicative noise for the mean-square loss. We use this property of the SGD noise to derive a stochastic differential equation (SDE) with simpler additive noise by performing a non-uniform transformation of the time variable. In the SDE, the gradient of the loss is replaced by that of the logarithmized loss. Consequently, we show that, near a local or global minimum, the stationary distribution $P_\mathrm{ss}(\theta)$ of the network parameters $\theta$ follows a power-law with respect to the loss function $L(\theta)$, i.e. $P_\mathrm{ss}(\theta)\propto L(\theta)^{-\phi}$ with the exponent $\phi$ specified by the mini-batch size, the learning rate, and the Hessian at the minimum. We obtain the escape rate formula from a local minimum, which is determined not by the loss barrier height $\Delta L=L(\theta^s)-L(\theta^*)$ between a minimum $\theta^*$ and a saddle $\theta^s$ but by the logarithmized loss barrier height $\Delta\log L=\log[L(\theta^s)/L(\theta^*)]$. Our escape-rate formula explains an empirical fact that SGD prefers flat minima with low effective dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge