On Minibatch Noise: Discrete-Time SGD, Overparametrization, and Bayes

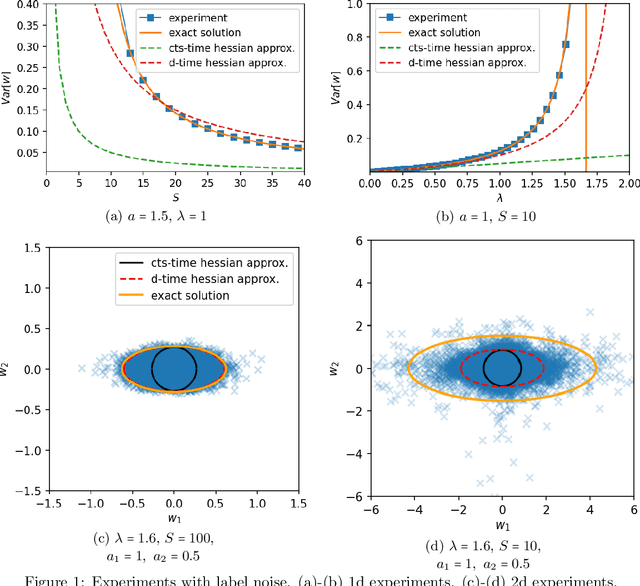
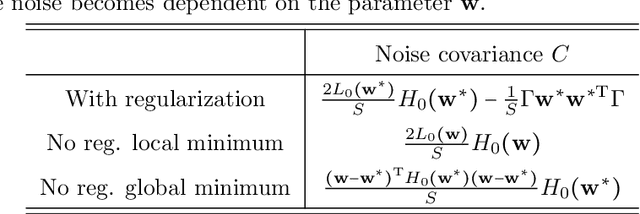
The noise in stochastic gradient descent (SGD), caused by minibatch sampling, remains poorly understood despite its enormous practical importance in offering good training efficiency and generalization ability. In this work, we study the minibatch noise in SGD. Motivated by the observation that minibatch sampling does not always cause a fluctuation, we set out to find the conditions that cause minibatch noise to emerge. We first derive the analytically solvable results for linear regression under various settings, which are compared to the commonly used approximations that are used to understand SGD noise. We show that some degree of mismatch between model and data complexity is needed in order for SGD to "cause" a noise, and that such mismatch may be due to the existence of static noise in the labels, in the input, the use of regularization, or underparametrization. Our results motivate a more accurate general formulation to describe minibatch noise.