Beyond adaptive gradient: Fast-Controlled Minibatch Algorithm for large-scale optimization

Adaptive gradient methods have been increasingly adopted by deep learning community due to their fast convergence and reduced sensitivity to hyper-parameters. However, these methods come with limitations, such as increased memory requirements for elements like moving averages and a poorly understood convergence theory. To overcome these challenges, we introduce F-CMA, a Fast-Controlled Mini-batch Algorithm with a random reshuffling method featuring a sufficient decrease condition and a line-search procedure to ensure loss reduction per epoch, along with its deterministic proof of global convergence to a stationary point. To evaluate the F-CMA, we integrate it into conventional training protocols for classification tasks involving both convolutional neural networks and vision transformer models, allowing for a direct comparison with popular optimizers. Computational tests show significant improvements, including a decrease in the overall training time by up to 68%, an increase in per-epoch efficiency by up to 20%, and in model accuracy by up to 5%.

Feature selection in linear SVMs via hard cardinality constraint: a scalable SDP decomposition approach

In this paper, we study the embedded feature selection problem in linear Support Vector Machines (SVMs), in which a cardinality constraint is employed, leading to a fully explainable selection model. The problem is NP-hard due to the presence of the cardinality constraint, even though the original linear SVM amounts to a problem solvable in polynomial time. To handle the hard problem, we first introduce two mixed-integer formulations for which novel SDP relaxations are proposed. Exploiting the sparsity pattern of the relaxations, we decompose the problems and obtain equivalent relaxations in a much smaller cone, making the conic approaches scalable. To make the best usage of the decomposed relaxations, we propose heuristics using the information of its optimal solution. Moreover, an exact procedure is proposed by solving a sequence of mixed-integer decomposed SDPs. Numerical results on classical benchmarking datasets are reported, showing the efficiency and effectiveness of our approach.

A graph neural network-based model with Out-of-Distribution Robustness for enhancing Antiretroviral Therapy Outcome Prediction for HIV-1

Predicting the outcome of antiretroviral therapies for HIV-1 is a pressing clinical challenge, especially when the treatment regimen includes drugs for which limited effectiveness data is available. This scarcity of data can arise either due to the introduction of a new drug to the market or due to limited use in clinical settings. To tackle this issue, we introduce a novel joint fusion model, which combines features from a Fully Connected (FC) Neural Network and a Graph Neural Network (GNN). The FC network employs tabular data with a feature vector made up of viral mutations identified in the most recent genotypic resistance test, along with the drugs used in therapy. Conversely, the GNN leverages knowledge derived from Stanford drug-resistance mutation tables, which serve as benchmark references for deducing in-vivo treatment efficacy based on the viral genetic sequence, to build informative graphs. We evaluated these models' robustness against Out-of-Distribution drugs in the test set, with a specific focus on the GNN's role in handling such scenarios. Our comprehensive analysis demonstrates that the proposed model consistently outperforms the FC model, especially when considering Out-of-Distribution drugs. These results underscore the advantage of integrating Stanford scores in the model, thereby enhancing its generalizability and robustness, but also extending its utility in real-world applications with limited data availability. This research highlights the potential of our approach to inform antiretroviral therapy outcome prediction and contribute to more informed clinical decisions.

Incorporating temporal dynamics of mutations to enhance the prediction capability of antiretroviral therapy's outcome for HIV-1

Motivation: In predicting HIV therapy outcomes, a critical clinical question is whether using historical information can enhance predictive capabilities compared with current or latest available data analysis. This study analyses whether historical knowledge, which includes viral mutations detected in all genotypic tests before therapy, their temporal occurrence, and concomitant viral load measurements, can bring improvements. We introduce a method to weigh mutations, considering the previously enumerated factors and the reference mutation-drug Stanford resistance tables. We compare a model encompassing history (H) with one not using it (NH). Results: The H-model demonstrates superior discriminative ability, with a higher ROC-AUC score (76.34%) than the NH-model (74.98%). Significant Wilcoxon test results confirm that incorporating historical information improves consistently predictive accuracy for treatment outcomes. The better performance of the H-model might be attributed to its consideration of latent HIV reservoirs, probably obtained when leveraging historical information. The findings emphasize the importance of temporal dynamics in mutations, offering insights into HIV infection complexities. However, our result also shows that prediction accuracy remains relatively high even when no historical information is available. Supplementary information: Supplementary material is available.

Unboxing Tree Ensembles for interpretability: a hierarchical visualization tool and a multivariate optimal re-built tree

The interpretability of models has become a crucial issue in Machine Learning because of algorithmic decisions' growing impact on real-world applications. Tree ensemble methods, such as Random Forests or XgBoost, are powerful learning tools for classification tasks. However, while combining multiple trees may provide higher prediction quality than a single one, it sacrifices the interpretability property resulting in "black-box" models. In light of this, we aim to develop an interpretable representation of a tree-ensemble model that can provide valuable insights into its behavior. First, given a target tree-ensemble model, we develop a hierarchical visualization tool based on a heatmap representation of the forest's feature use, considering the frequency of a feature and the level at which it is selected as an indicator of importance. Next, we propose a mixed-integer linear programming (MILP) formulation for constructing a single optimal multivariate tree that accurately mimics the target model predictions. The goal is to provide an interpretable surrogate model based on oblique hyperplane splits, which uses only the most relevant features according to the defined forest's importance indicators. The MILP model includes a penalty on feature selection based on their frequency in the forest to further induce sparsity of the splits. The natural formulation has been strengthened to improve the computational performance of mixed-integer software. Computational experience is carried out on benchmark datasets from the UCI repository using a state-of-the-art off-the-shelf solver. Results show that the proposed model is effective in yielding a shallow interpretable tree approximating the tree-ensemble decision function.

Convergence under Lipschitz smoothness of ease-controlled Random Reshuffling gradient Algorithms

We consider minimizing the average of a very large number of smooth and possibly non-convex functions. This optimization problem has deserved much attention in the past years due to the many applications in different fields, the most challenging being training Machine Learning models. Widely used approaches for solving this problem are mini-batch gradient methods which, at each iteration, update the decision vector moving along the gradient of a mini-batch of the component functions. We consider the Incremental Gradient (IG) and the Random reshuffling (RR) methods which proceed in cycles, picking batches in a fixed order or by reshuffling the order after each epoch. Convergence properties of these schemes have been proved under different assumptions, usually quite strong. We aim to define ease-controlled modifications of the IG/RR schemes, which require a light additional computational effort and can be proved to converge under very weak and standard assumptions. In particular, we define two algorithmic schemes, monotone or non-monotone, in which the IG/RR iteration is controlled by using a watchdog rule and a derivative-free line search that activates only sporadically to guarantee convergence. The two schemes also allow controlling the updating of the stepsize used in the main IG/RR iteration, avoiding the use of preset rules. We prove convergence under the lonely assumption of Lipschitz continuity of the gradients of the component functions and perform extensive computational analysis using Deep Neural Architectures and a benchmark of datasets. We compare our implementation with both full batch gradient methods and online standard implementation of IG/RR methods, proving that the computational effort is comparable with the corresponding online methods and that the control on the learning rate may allow faster decrease.

Margin Optimal Classification Trees

In recent years there has been growing attention to interpretable machine learning models which can give explanatory insights on their behavior. Thanks to their interpretability, decision trees have been intensively studied for classification tasks, and due to the remarkable advances in mixed-integer programming (MIP), various approaches have been proposed to formulate the problem of training an Optimal Classification Tree (OCT) as a MIP model. We present a novel mixed-integer quadratic formulation for the OCT problem, which exploits the generalization capabilities of Support Vector Machines for binary classification. Our model, denoted as Margin Optimal Classification Tree (MARGOT), encompasses the use of maximum margin multivariate hyperplanes nested in a binary tree structure. To enhance the interpretability of our approach, we analyse two alternative versions of MARGOT, which include feature selection constraints inducing local sparsity of the hyperplanes. First, MARGOT has been tested on non-linearly separable synthetic datasets in 2-dimensional feature space to provide a graphical representation of the maximum margin approach. Finally, the proposed models have been tested on benchmark datasets from the UCI repository. The MARGOT formulation turns out to be easier to solve than other OCT approaches, and the generated tree better generalizes on new observations. The two interpretable versions are effective in selecting the most relevant features and maintaining good prediction quality.

Solving the vehicle routing problem with deep reinforcement learning

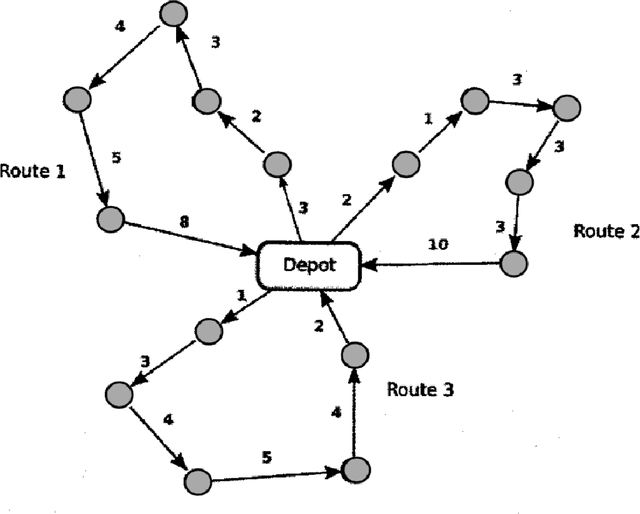
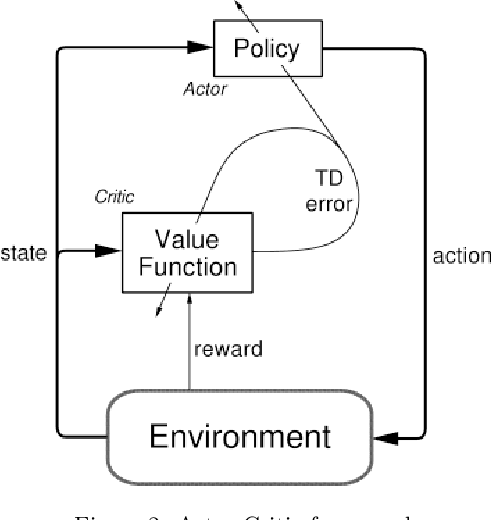
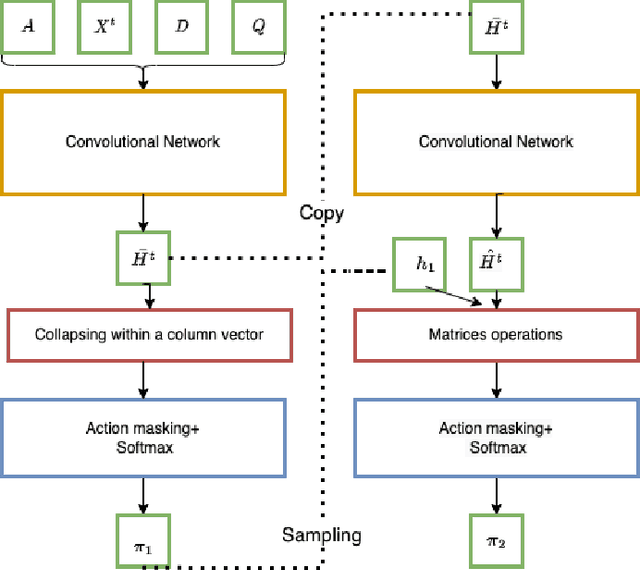
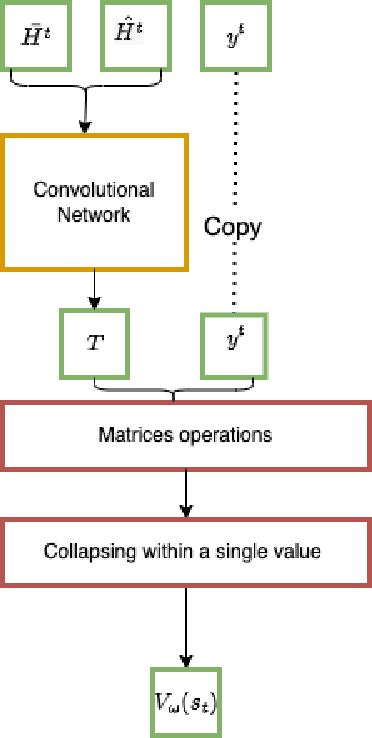
Recently, the applications of the methodologies of Reinforcement Learning (RL) to NP-Hard Combinatorial optimization problems have become a popular topic. This is essentially due to the nature of the traditional combinatorial algorithms, often based on a trial-and-error process. RL aims at automating this process. At this regard, this paper focuses on the application of RL for the Vehicle Routing Problem (VRP), a famous combinatorial problem that belongs to the class of NP-Hard problems. In this work, first, the problem is modeled as a Markov Decision Process (MDP) and then the PPO method (which belongs to the Actor-Critic class of Reinforcement learning methods) is applied. In a second phase, the neural architecture behind the Actor and Critic has been established, choosing to adopt a neural architecture based on the Convolutional neural networks, both for the Actor and the Critic. This choice resulted in effectively addressing problems of different sizes. Experiments performed on a wide range of instances show that the algorithm has good generalization capabilities and can reach good solutions in a short time. Comparisons between the algorithm proposed and the state-of-the-art solver OR-TOOLS show that the latter still outperforms the Reinforcement learning algorithm. However, there are future research perspectives, that aim to upgrade the current performance of the algorithm proposed.

AI-based Data Preparation and Data Analytics in Healthcare: The Case of Diabetes

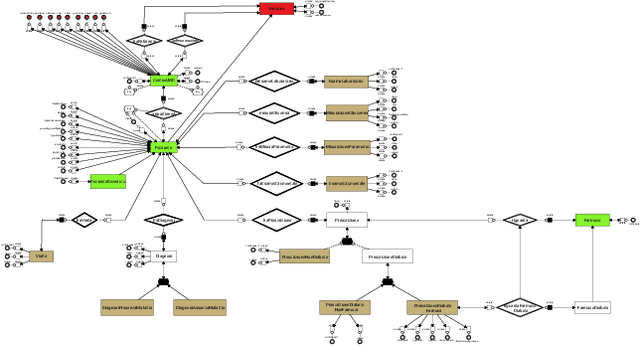
The Associazione Medici Diabetologi (AMD) collects and manages one of the largest worldwide-available collections of diabetic patient records, also known as the AMD database. This paper presents the initial results of an ongoing project whose focus is the application of Artificial Intelligence and Machine Learning techniques for conceptualizing, cleaning, and analyzing such an important and valuable dataset, with the goal of providing predictive insights to better support diabetologists in their diagnostic and therapeutic choices.

Block Layer Decomposition schemes for training Deep Neural Networks

Deep Feedforward Neural Networks' (DFNNs) weights estimation relies on the solution of a very large nonconvex optimization problem that may have many local (no global) minimizers, saddle points and large plateaus. As a consequence, optimization algorithms can be attracted toward local minimizers which can lead to bad solutions or can slow down the optimization process. Furthermore, the time needed to find good solutions to the training problem depends on both the number of samples and the number of variables. In this work, we show how Block Coordinate Descent (BCD) methods can be applied to improve performance of state-of-the-art algorithms by avoiding bad stationary points and flat regions. We first describe a batch BCD method ables to effectively tackle the network's depth and then we further extend the algorithm proposing a \textit{minibatch} BCD framework able to scale with respect to both the number of variables and the number of samples by embedding a BCD approach into a minibatch framework. By extensive numerical results on standard datasets for several architecture networks, we show how the application of BCD methods to the training phase of DFNNs permits to outperform standard batch and minibatch algorithms leading to an improvement on both the training phase and the generalization performance of the networks.