Beyond adaptive gradient: Fast-Controlled Minibatch Algorithm for large-scale optimization

Adaptive gradient methods have been increasingly adopted by deep learning community due to their fast convergence and reduced sensitivity to hyper-parameters. However, these methods come with limitations, such as increased memory requirements for elements like moving averages and a poorly understood convergence theory. To overcome these challenges, we introduce F-CMA, a Fast-Controlled Mini-batch Algorithm with a random reshuffling method featuring a sufficient decrease condition and a line-search procedure to ensure loss reduction per epoch, along with its deterministic proof of global convergence to a stationary point. To evaluate the F-CMA, we integrate it into conventional training protocols for classification tasks involving both convolutional neural networks and vision transformer models, allowing for a direct comparison with popular optimizers. Computational tests show significant improvements, including a decrease in the overall training time by up to 68%, an increase in per-epoch efficiency by up to 20%, and in model accuracy by up to 5%.

Solving the vehicle routing problem with deep reinforcement learning

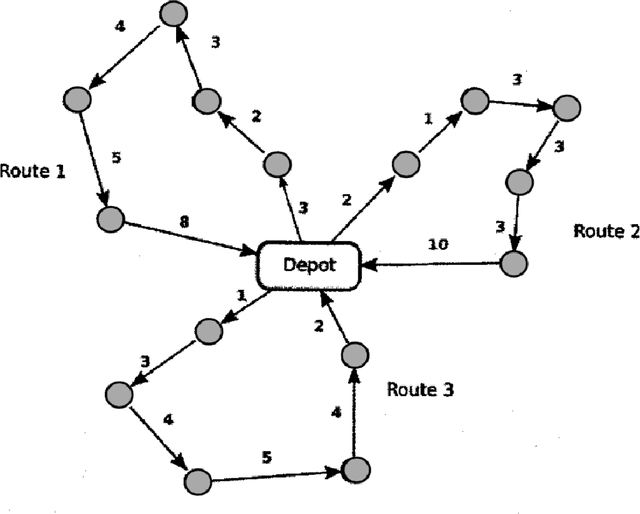
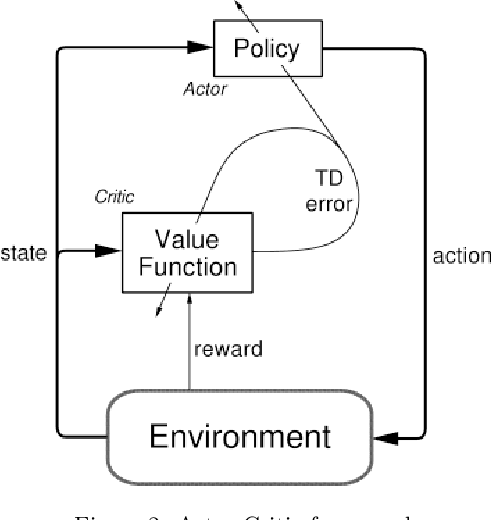
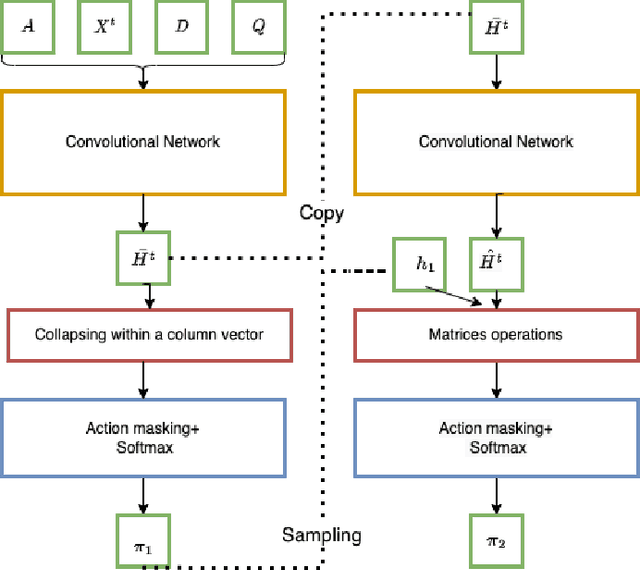
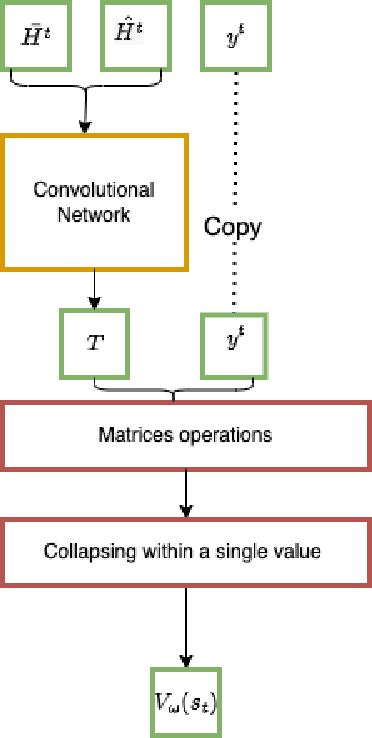
Recently, the applications of the methodologies of Reinforcement Learning (RL) to NP-Hard Combinatorial optimization problems have become a popular topic. This is essentially due to the nature of the traditional combinatorial algorithms, often based on a trial-and-error process. RL aims at automating this process. At this regard, this paper focuses on the application of RL for the Vehicle Routing Problem (VRP), a famous combinatorial problem that belongs to the class of NP-Hard problems. In this work, first, the problem is modeled as a Markov Decision Process (MDP) and then the PPO method (which belongs to the Actor-Critic class of Reinforcement learning methods) is applied. In a second phase, the neural architecture behind the Actor and Critic has been established, choosing to adopt a neural architecture based on the Convolutional neural networks, both for the Actor and the Critic. This choice resulted in effectively addressing problems of different sizes. Experiments performed on a wide range of instances show that the algorithm has good generalization capabilities and can reach good solutions in a short time. Comparisons between the algorithm proposed and the state-of-the-art solver OR-TOOLS show that the latter still outperforms the Reinforcement learning algorithm. However, there are future research perspectives, that aim to upgrade the current performance of the algorithm proposed.

PUSH: a primal heuristic based on Feasibility PUmp and SHifting

This work describes PUSH, a primal heuristic combining Feasibility Pump and Shifting. The main idea is to replace the rounding phase of the Feasibility Pump with a suitable adaptation of the Shifting and other rounding heuristics. The algorithm presents different strategies, depending on the nature of the partial rounding obtained. In particular, we distinguish when the partial solution is feasible, infeasible with potential candidates, and infeasible without candidates. We used a threshold to indicate the percentage of variables to round with our algorithm and which other to round to the nearest integer. Most importantly, our algorithm tackles directly equality constraints without duplicating rows. We select the parameters of our algorithm on the 19 instances provided for the Mip Competition 2022. Finally, we compared our approach to other start heuristics, like Simple Rounding, Rounding, Shifting, and Feasibility Pump on the first 800 MIPLIB2017 instances ordered by the number of non-zeros.