Ruggiero Seccia
Convergence under Lipschitz smoothness of ease-controlled Random Reshuffling gradient Algorithms
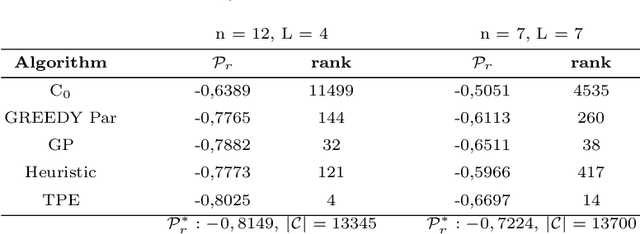
Dec 04, 2022Abstract:We consider minimizing the average of a very large number of smooth and possibly non-convex functions. This optimization problem has deserved much attention in the past years due to the many applications in different fields, the most challenging being training Machine Learning models. Widely used approaches for solving this problem are mini-batch gradient methods which, at each iteration, update the decision vector moving along the gradient of a mini-batch of the component functions. We consider the Incremental Gradient (IG) and the Random reshuffling (RR) methods which proceed in cycles, picking batches in a fixed order or by reshuffling the order after each epoch. Convergence properties of these schemes have been proved under different assumptions, usually quite strong. We aim to define ease-controlled modifications of the IG/RR schemes, which require a light additional computational effort and can be proved to converge under very weak and standard assumptions. In particular, we define two algorithmic schemes, monotone or non-monotone, in which the IG/RR iteration is controlled by using a watchdog rule and a derivative-free line search that activates only sporadically to guarantee convergence. The two schemes also allow controlling the updating of the stepsize used in the main IG/RR iteration, avoiding the use of preset rules. We prove convergence under the lonely assumption of Lipschitz continuity of the gradients of the component functions and perform extensive computational analysis using Deep Neural Architectures and a benchmark of datasets. We compare our implementation with both full batch gradient methods and online standard implementation of IG/RR methods, proving that the computational effort is comparable with the corresponding online methods and that the control on the learning rate may allow faster decrease.
Block Layer Decomposition schemes for training Deep Neural Networks
Mar 18, 2020



Abstract:Deep Feedforward Neural Networks' (DFNNs) weights estimation relies on the solution of a very large nonconvex optimization problem that may have many local (no global) minimizers, saddle points and large plateaus. As a consequence, optimization algorithms can be attracted toward local minimizers which can lead to bad solutions or can slow down the optimization process. Furthermore, the time needed to find good solutions to the training problem depends on both the number of samples and the number of variables. In this work, we show how Block Coordinate Descent (BCD) methods can be applied to improve performance of state-of-the-art algorithms by avoiding bad stationary points and flat regions. We first describe a batch BCD method ables to effectively tackle the network's depth and then we further extend the algorithm proposing a \textit{minibatch} BCD framework able to scale with respect to both the number of variables and the number of samples by embedding a BCD approach into a minibatch framework. By extensive numerical results on standard datasets for several architecture networks, we show how the application of BCD methods to the training phase of DFNNs permits to outperform standard batch and minibatch algorithms leading to an improvement on both the training phase and the generalization performance of the networks.
* 23 pages
A gray-box approach for curriculum learning
Jun 17, 2019
Abstract:Curriculum learning is often employed in deep reinforcement learning to let the agent progress more quickly towards better behaviors. Numerical methods for curriculum learning in the literature provides only initial heuristic solutions, with little to no guarantee on their quality. We define a new gray-box function that, including a suitable scheduling problem, can be effectively used to reformulate the curriculum learning problem. We propose different efficient numerical methods to address this gray-box reformulation. Preliminary numerical results on a benchmark task in the curriculum learning literature show the viability of the proposed approach.
* 10 pages, 1 figure
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge