Spatially-guided Temporal Aggregation for Robust Event-RGB Optical Flow Estimation

Current optical flow methods exploit the stable appearance of frame (or RGB) data to establish robust correspondences across time. Event cameras, on the other hand, provide high-temporal-resolution motion cues and excel in challenging scenarios. These complementary characteristics underscore the potential of integrating frame and event data for optical flow estimation. However, most cross-modal approaches fail to fully utilize the complementary advantages, relying instead on simply stacking information. This study introduces a novel approach that uses a spatially dense modality to guide the aggregation of the temporally dense event modality, achieving effective cross-modal fusion. Specifically, we propose an event-enhanced frame representation that preserves the rich texture of frames and the basic structure of events. We use the enhanced representation as the guiding modality and employ events to capture temporally dense motion information. The robust motion features derived from the guiding modality direct the aggregation of motion information from events. To further enhance fusion, we propose a transformer-based module that complements sparse event motion features with spatially rich frame information and enhances global information propagation. Additionally, a mix-fusion encoder is designed to extract comprehensive spatiotemporal contextual features from both modalities. Extensive experiments on the MVSEC and DSEC-Flow datasets demonstrate the effectiveness of our framework. Leveraging the complementary strengths of frames and events, our method achieves leading performance on the DSEC-Flow dataset. Compared to the event-only model, frame guidance improves accuracy by 10\%. Furthermore, it outperforms the state-of-the-art fusion-based method with a 4\% accuracy gain and a 45\% reduction in inference time.

ResFlow: Fine-tuning Residual Optical Flow for Event-based High Temporal Resolution Motion Estimation

Event cameras hold significant promise for high-temporal-resolution (HTR) motion estimation. However, estimating event-based HTR optical flow faces two key challenges: the absence of HTR ground-truth data and the intrinsic sparsity of event data. Most existing approaches rely on the flow accumulation paradigms to indirectly supervise intermediate flows, often resulting in accumulation errors and optimization difficulties. To address these challenges, we propose a residual-based paradigm for estimating HTR optical flow with event data. Our approach separates HTR flow estimation into two stages: global linear motion estimation and HTR residual flow refinement. The residual paradigm effectively mitigates the impacts of event sparsity on optimization and is compatible with any LTR algorithm. Next, to address the challenge posed by the absence of HTR ground truth, we incorporate novel learning strategies. Specifically, we initially employ a shared refiner to estimate the residual flows, enabling both LTR supervision and HTR inference. Subsequently, we introduce regional noise to simulate the residual patterns of intermediate flows, facilitating the adaptation from LTR supervision to HTR inference. Additionally, we show that the noise-based strategy supports in-domain self-supervised training. Comprehensive experimental results demonstrate that our approach achieves state-of-the-art accuracy in both LTR and HTR metrics, highlighting its effectiveness and superiority.

Motion Control of Two Mobile Robots under Allowable Collisions

This letter investigates the motion control problem of two mobile robots under allowable collisions. Here, the allowable collisions mean that the collisions do not damage the mobile robots. The occurrence of the collisions is discussed and the effects of the collisions on the mobile robots are analyzed to develop a hybrid model of each mobile robot under allowable collisions. Based on the effects of the collisions, we show the necessity of redesigning the motion control strategy for mobile robots. Furthermore, impulsive control techniques are applied to redesign the motion control strategy to guarantee the task accomplishment for each mobile robot. Finally, an example is used to illustrate the redesigned motion control strategy.

Optimal Estimator Design and Properties Analysis for Interconnected Systems with Asymmetric Information Structure

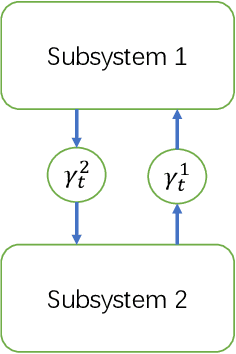
This paper studies the optimal state estimation problem for interconnected systems. Each subsystem can obtain its own measurement in real time, while, the measurements transmitted between the subsystems suffer from random delay. The optimal estimator is analytically designed for minimizing the conditional error covariance. Due to the random delay, the error covariance of the estimation is random. The boundedness of the expected error covariance (EEC) is analyzed. In particular, a new condition that is easy to verify is established for the boundedness of EEC. Further, the properties about EEC with respect to the delay probability is studied. We found that there exists a critical probability such that the EEC is bounded if the delay probability is below the critical probability. Also, a lower and upper bound of the critical probability is effectively computed. Finally, the proposed results are applied to a power system, and the effectiveness of the designed methods is illustrated by simulations.

Average Cost Optimal Control of Stochastic Systems Using Reinforcement Learning

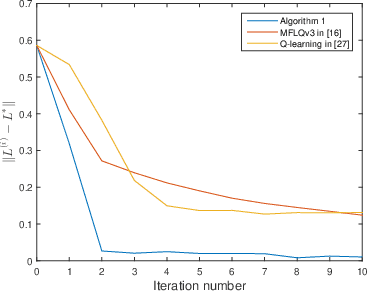
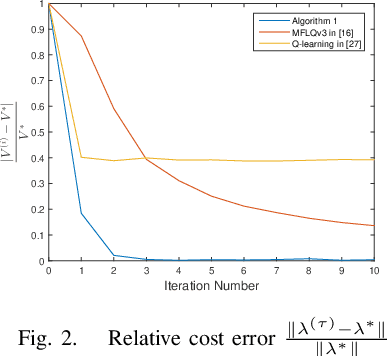
This paper addresses the average cost minimization problem for discrete-time systems with multiplicative and additive noises via reinforcement learning. By using Q-function, we propose an online learning scheme to estimate the kernel matrix of Q-function and to update the control gain using the data along the system trajectories. The obtained control gain and kernel matrix are proved to converge to the optimal ones. To implement the proposed learning scheme, an online model-free reinforcement learning algorithm is given, where recursive least squares method is used to estimate the kernel matrix of Q-function. A numerical example is presented to illustrate the proposed approach.

Model-free optimal control of discrete-time systems with additive and multiplicative noises

This paper investigates the optimal control problem for a class of discrete-time stochastic systems subject to additive and multiplicative noises. A stochastic Lyapunov equation and a stochastic algebra Riccati equation are established for the existence of the optimal admissible control policy. A model-free reinforcement learning algorithm is proposed to learn the optimal admissible control policy using the data of the system states and inputs without requiring any knowledge of the system matrices. It is proven that the learning algorithm converges to the optimal admissible control policy. The implementation of the model-free algorithm is based on batch least squares and numerical average. The proposed algorithm is illustrated through a numerical example, which shows our algorithm outperforms other policy iteration algorithms.