Optimal Estimator Design and Properties Analysis for Interconnected Systems with Asymmetric Information Structure

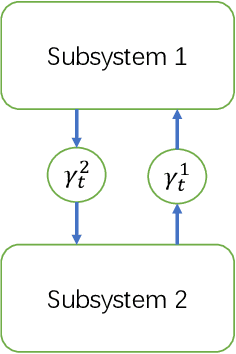
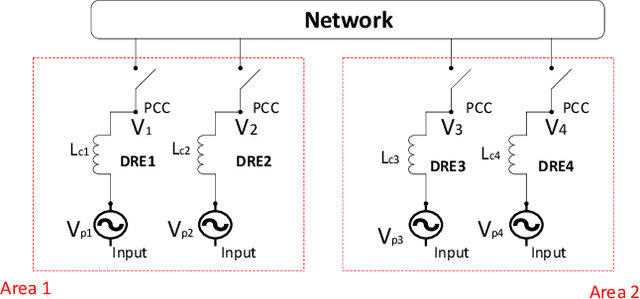
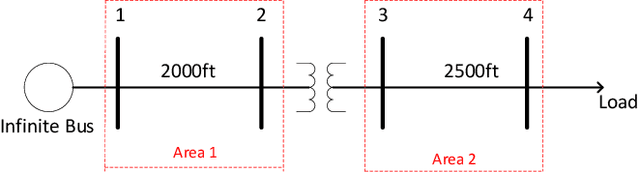
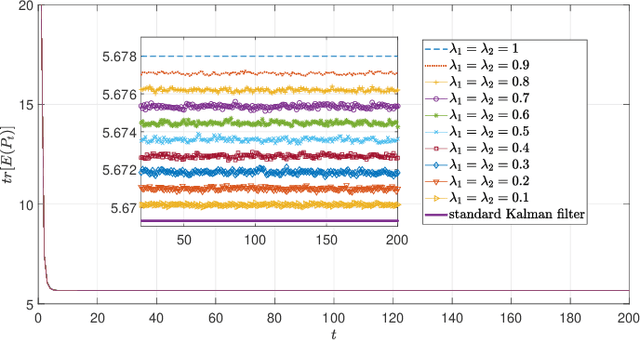
This paper studies the optimal state estimation problem for interconnected systems. Each subsystem can obtain its own measurement in real time, while, the measurements transmitted between the subsystems suffer from random delay. The optimal estimator is analytically designed for minimizing the conditional error covariance. Due to the random delay, the error covariance of the estimation is random. The boundedness of the expected error covariance (EEC) is analyzed. In particular, a new condition that is easy to verify is established for the boundedness of EEC. Further, the properties about EEC with respect to the delay probability is studied. We found that there exists a critical probability such that the EEC is bounded if the delay probability is below the critical probability. Also, a lower and upper bound of the critical probability is effectively computed. Finally, the proposed results are applied to a power system, and the effectiveness of the designed methods is illustrated by simulations.