Average Cost Optimal Control of Stochastic Systems Using Reinforcement Learning

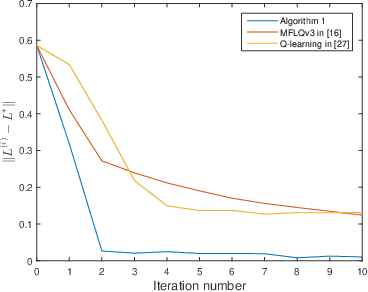
This paper addresses the average cost minimization problem for discrete-time systems with multiplicative and additive noises via reinforcement learning. By using Q-function, we propose an online learning scheme to estimate the kernel matrix of Q-function and to update the control gain using the data along the system trajectories. The obtained control gain and kernel matrix are proved to converge to the optimal ones. To implement the proposed learning scheme, an online model-free reinforcement learning algorithm is given, where recursive least squares method is used to estimate the kernel matrix of Q-function. A numerical example is presented to illustrate the proposed approach.

Model-free optimal control of discrete-time systems with additive and multiplicative noises

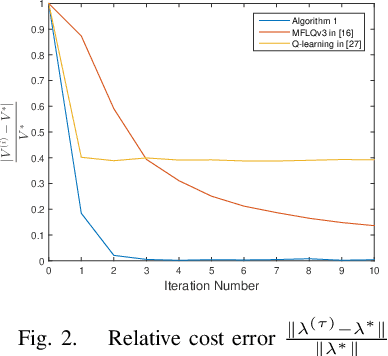
This paper investigates the optimal control problem for a class of discrete-time stochastic systems subject to additive and multiplicative noises. A stochastic Lyapunov equation and a stochastic algebra Riccati equation are established for the existence of the optimal admissible control policy. A model-free reinforcement learning algorithm is proposed to learn the optimal admissible control policy using the data of the system states and inputs without requiring any knowledge of the system matrices. It is proven that the learning algorithm converges to the optimal admissible control policy. The implementation of the model-free algorithm is based on batch least squares and numerical average. The proposed algorithm is illustrated through a numerical example, which shows our algorithm outperforms other policy iteration algorithms.