Brain-Inspired Spike Echo State Network Dynamics for Aero-Engine Intelligent Fault Prediction

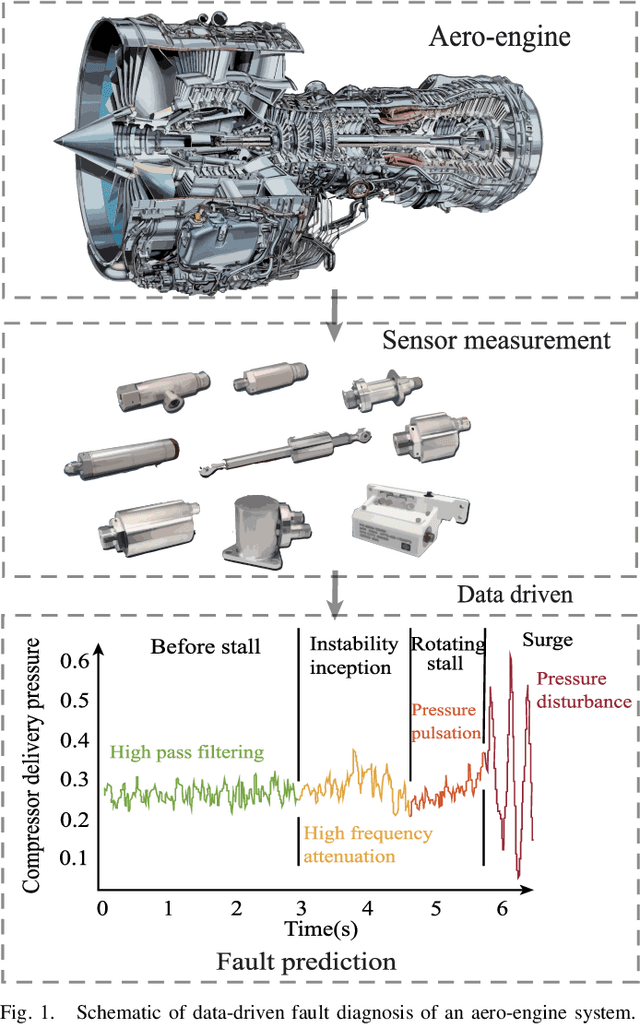
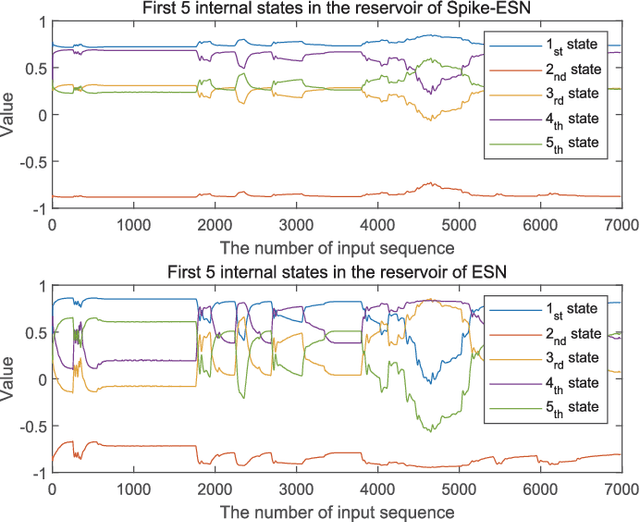
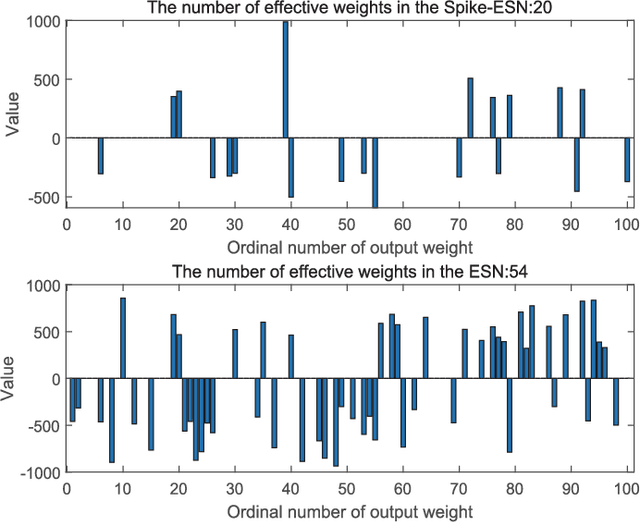
Aero-engine fault prediction aims to accurately predict the development trend of the future state of aero-engines, so as to diagnose faults in advance. Traditional aero-engine parameter prediction methods mainly use the nonlinear mapping relationship of time series data but generally ignore the adequate spatiotemporal features contained in aero-engine data. To this end, we propose a brain-inspired spike echo state network (Spike-ESN) model for aero-engine intelligent fault prediction, which is used to effectively capture the evolution process of aero-engine time series data in the framework of spatiotemporal dynamics. In the proposed approach, we design a spike input layer based on Poisson distribution inspired by the spike neural encoding mechanism of biological neurons, which can extract the useful temporal characteristics in aero-engine sequence data. Then, the temporal characteristics are input into a spike reservoir through the current calculation method of spike accumulation in neurons, which projects the data into a high-dimensional sparse space. In addition, we use the ridge regression method to read out the internal state of the spike reservoir. Finally, the experimental results of aero-engine states prediction demonstrate the superiority and potential of the proposed method.

Physically Informed Synchronic-adaptive Learning for Industrial Systems Modeling in Heterogeneous Media with Unavailable Time-varying Interface

Partial differential equations (PDEs) are commonly employed to model complex industrial systems characterized by multivariable dependence. Existing physics-informed neural networks (PINNs) excel in solving PDEs in a homogeneous medium. However, their feasibility is diminished when PDE parameters are unknown due to a lack of physical attributions and time-varying interface is unavailable arising from heterogeneous media. To this end, we propose a data-physics-hybrid method, physically informed synchronic-adaptive learning (PISAL), to solve PDEs for industrial systems modeling in heterogeneous media. First, Net1, Net2, and NetI, are constructed to approximate the solutions satisfying PDEs and the interface. Net1 and Net2 are utilized to synchronously learn each solution satisfying PDEs with diverse parameters, while NetI is employed to adaptively learn the unavailable time-varying interface. Then, a criterion combined with NetI is introduced to adaptively distinguish the attributions of measurements and collocation points. Furthermore, NetI is integrated into a data-physics-hybrid loss function. Accordingly, a synchronic-adaptive learning (SAL) strategy is proposed to decompose and optimize each subdomain. Besides, we theoretically prove the approximation capability of PISAL. Extensive experimental results verify that the proposed PISAL can be used for industrial systems modeling in heterogeneous media, which faces the challenges of lack of physical attributions and unavailable time-varying interface.

Motion Control of Two Mobile Robots under Allowable Collisions

This letter investigates the motion control problem of two mobile robots under allowable collisions. Here, the allowable collisions mean that the collisions do not damage the mobile robots. The occurrence of the collisions is discussed and the effects of the collisions on the mobile robots are analyzed to develop a hybrid model of each mobile robot under allowable collisions. Based on the effects of the collisions, we show the necessity of redesigning the motion control strategy for mobile robots. Furthermore, impulsive control techniques are applied to redesign the motion control strategy to guarantee the task accomplishment for each mobile robot. Finally, an example is used to illustrate the redesigned motion control strategy.

PDE Discovery for Soft Sensors Using Coupled Physics-Informed Neural Network with Akaike's Information Criterion

Soft sensors have been extensively used to monitor key variables using easy-to-measure variables and mathematical models. Partial differential equations (PDEs) are model candidates for soft sensors in industrial processes with spatiotemporal dependence. However, gaps often exist between idealized PDEs and practical situations. Discovering proper structures of PDEs, including the differential operators and source terms, can remedy the gaps. To this end, a coupled physics-informed neural network with Akaike's criterion information (CPINN-AIC) is proposed for PDE discovery of soft sensors. First, CPINN is adopted for obtaining solutions and source terms satisfying PDEs. Then, we propose a data-physics-hybrid loss function for training CPINN, in which undetermined combinations of differential operators are involved. Consequently, AIC is used to discover the proper combination of differential operators. Finally, the artificial and practical datasets are used to verify the feasibility and effectiveness of CPINN-AIC for soft sensors. The proposed CPINN-AIC is a data-driven method to discover proper PDE structures and neural network-based solutions for soft sensors.

Coupled Physics-informed Neural Networks for Inferring Solutions of Partial Differential Equations with Unknown Source Terms

Physics-informed neural networks (PINNs) provide a transformative development for approximating the solutions to partial differential equations (PDEs). This work proposes a coupled physics-informed neural network (C-PINN) for the nonhomogeneous PDEs with unknown dynamical source terms, which is used to describe the systems with external forces and cannot be well approximated by the existing PINNs. In our method, two neural networks, NetU and NetG, are proposed. NetU is constructed to generate a quasi-solution satisfying PDEs under study. NetG is used to regularize the training of NetU. Then, the two networks are integrated into a data-physics-hybrid cost function. Finally, we propose a hierarchical training strategy to optimize and couple the two networks. The performance of C-PINN is proved by approximating several classical PDEs.