Is Pontryagin's Maximum Principle all you need? Solving optimal control problems with PMP-inspired neural networks

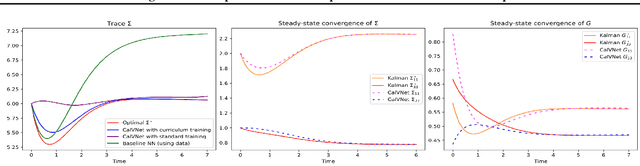
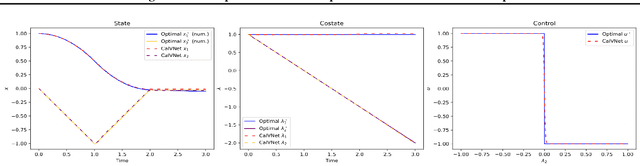
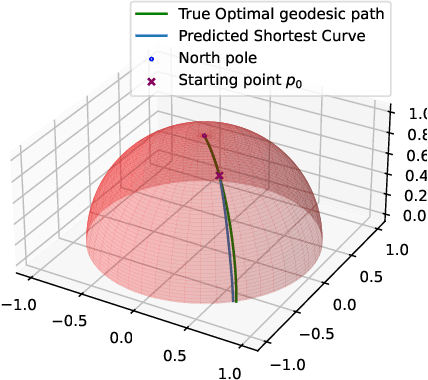
Calculus of Variations is the mathematics of functional optimization, i.e., when the solutions are functions over a time interval. This is particularly important when the time interval is unknown like in minimum-time control problems, so that forward in time solutions are not possible. Calculus of Variations offers a robust framework for learning optimal control and inference. How can this framework be leveraged to design neural networks to solve challenges in control and inference? We propose the Pontryagin's Maximum Principle Neural Network (PMP-net) that is tailored to estimate control and inference solutions, in accordance with the necessary conditions outlined by Pontryagin's Maximum Principle. We assess PMP-net on two classic optimal control and inference problems: optimal linear filtering and minimum-time control. Our findings indicate that PMP-net can be effectively trained in an unsupervised manner to solve these problems without the need for ground-truth data, successfully deriving the classical "Kalman filter" and "bang-bang" control solution. This establishes a new approach for addressing general, possibly yet unsolved, optimal control problems.

PhyOT: Physics-informed object tracking in surveillance cameras

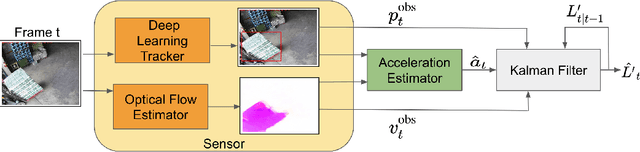
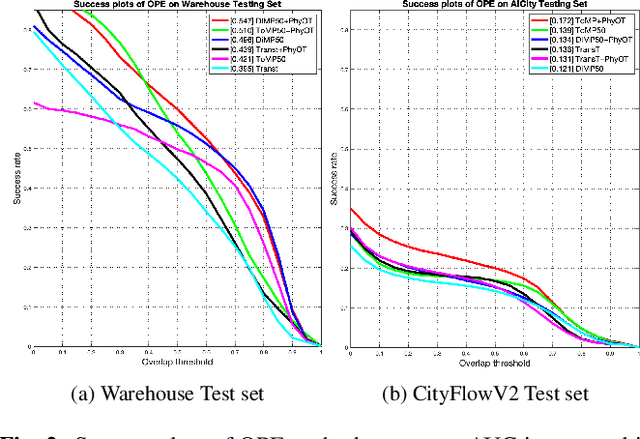
While deep learning has been very successful in computer vision, real world operating conditions such as lighting variation, background clutter, or occlusion hinder its accuracy across several tasks. Prior work has shown that hybrid models -- combining neural networks and heuristics/algorithms -- can outperform vanilla deep learning for several computer vision tasks, such as classification or tracking. We consider the case of object tracking, and evaluate a hybrid model (PhyOT) that conceptualizes deep neural networks as ``sensors'' in a Kalman filter setup, where prior knowledge, in the form of Newtonian laws of motion, is used to fuse sensor observations and to perform improved estimations. Our experiments combine three neural networks, performing position, indirect velocity and acceleration estimation, respectively, and evaluate such a formulation on two benchmark datasets: a warehouse security camera dataset that we collected and annotated and a traffic camera open dataset. Results suggest that our PhyOT can track objects in extreme conditions that the state-of-the-art deep neural networks fail while its performance in general cases does not degrade significantly from that of existing deep learning approaches. Results also suggest that our PhyOT components are generalizable and transferable.

GSP = DSP + Boundary Conditions -- The Graph Signal Processing Companion Model

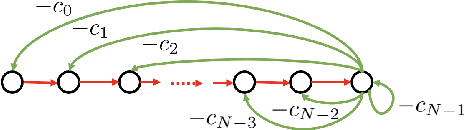
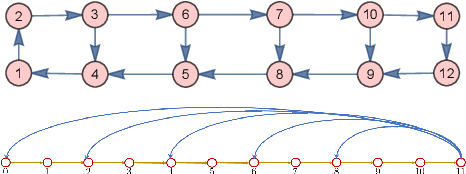
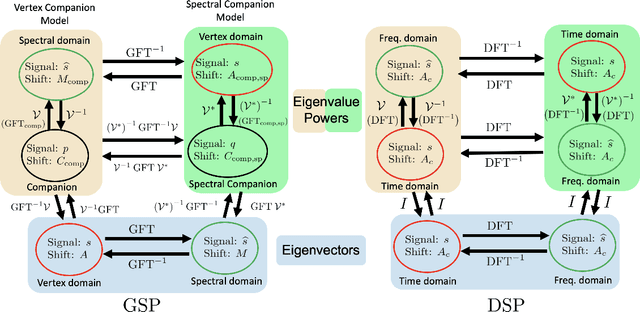
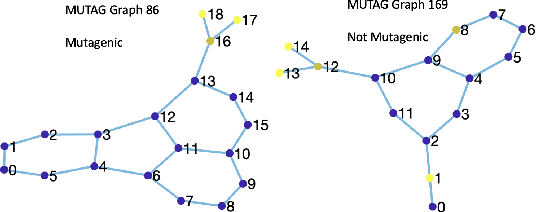
The paper presents the graph signal processing (GSP) companion model that naturally replicates the basic tenets of classical signal processing (DSP) for GSP. The companion model shows that GSP can be made equivalent to DSP 'plus' appropriate boundary conditions (bc) - this is shown under broad conditions and holds for arbitrary undirected or directed graphs. This equivalence suggests how to broaden GSP - extend naturally a DSP concept to the GSP companion model and then transfer it back to the common graph vertex and graph Fourier domains. The paper shows that GSP unrolls as two distinct models that coincide in DSP, the companion model based on (Hadamard or pointwise) powers of what we will introduce as the spectral frequency vector $\lambda$, and the traditional graph vertex model, based on the adjacency matrix and its eigenvectors. The paper expands GSP in several directions, including showing that convolution in the graph companion model can be achieved with the FFT and that GSP modulation with appropriate choice of carriers exhibits the DSP translation effect that enables multiplexing by modulation of graph signals.

The Companion Model -- a Canonical Model in Graph Signal Processing

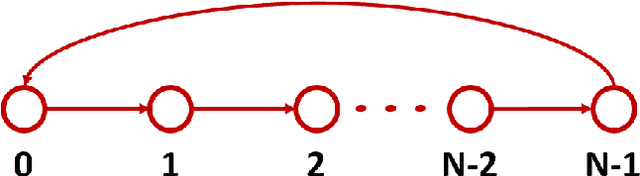
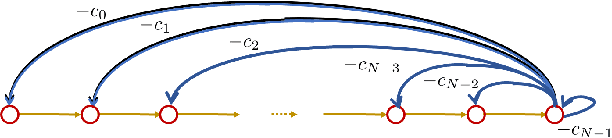
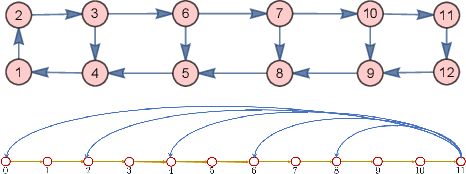
This paper introduces a $\textit{canonical}$ graph signal model defined by a $\textit{canonical}$ graph and a $\textit{canonical}$ shift, the $\textit{companion}$ graph and the $\textit{companion}$ shift. These are canonical because, under standard conditions, we show that any graph signal processing (GSP) model can be transformed into the canonical model. The transform that obtains this is the graph $z$-transform ($\textrm{G$z$T}$) that we introduce. The GSP canonical model comes closest to the discrete signal processing (DSP) time signal models: the structure of the companion shift decomposes into a line shift and a signal continuation just like the DSP shift and the GSP canonical graph is a directed line graph with a terminal condition reflecting the signal continuation condition. We further show that, surprisingly, in the canonical model, convolution of graph signals is fast convolution by the DSP FFT.

Shuffler: A Large Scale Data Management Tool for ML in Computer Vision

Datasets in the computer vision academic research community are primarily static. Once a dataset is accepted as a benchmark for a computer vision task, researchers working on this task will not alter it in order to make their results reproducible. At the same time, when exploring new tasks and new applications, datasets tend to be an ever changing entity. A practitioner may combine existing public datasets, filter images or objects in them, change annotations or add new ones to fit a task at hand, visualize sample images, or perhaps output statistics in the form of text or plots. In fact, datasets change as practitioners experiment with data as much as with algorithms, trying to make the most out of machine learning models. Given that ML and deep learning call for large volumes of data to produce satisfactory results, it is no surprise that the resulting data and software management associated to dealing with live datasets can be quite complex. As far as we know, there is no flexible, publicly available instrument to facilitate manipulating image data and their annotations throughout a ML pipeline. In this work, we present Shuffler, an open source tool that makes it easy to manage large computer vision datasets. It stores annotations in a relational, human-readable database. Shuffler defines over 40 data handling operations with annotations that are commonly useful in supervised learning applied to computer vision and supports some of the most well-known computer vision datasets. Finally, it is easily extensible, making the addition of new operations and datasets a task that is fast and easy to accomplish.

Graph Signal Processing: A Signal Representation Approach to Convolution and Sampling

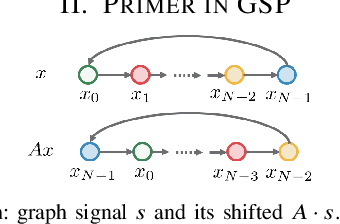
The paper presents sampling in GSP as 1) linear operations (change of bases) between signal representations and 2) downsampling as linear shift invariant filtering and reconstruction (interpolation) as filtering, both in the spectral domain. To achieve this, it considers a spectral shift $M$ that leads to a spectral graph signal processing theory, $\text{GSP}_{\textrm{sp}}$, dual to GSP but that starts from the spectral domain and $M$. The paper introduces alternative signal representations, convolution of graph signals for these alternative representations, presenting a $\textit{fast}$ GSP convolution that uses the DSP FFT algorithm, and sampling as solutions of algebraic linear systems of equations.

Towards Aggregating Weighted Feature Attributions

Current approaches for explaining machine learning models fall into two distinct classes: antecedent event influence and value attribution. The former leverages training instances to describe how much influence a training point exerts on a test point, while the latter attempts to attribute value to the features most pertinent to a given prediction. In this work, we discuss an algorithm, AVA: Aggregate Valuation of Antecedents, that fuses these two explanation classes to form a new approach to feature attribution that not only retrieves local explanations but also captures global patterns learned by a model. Our experimentation convincingly favors weighting and aggregating feature attributions via AVA.

Topology Adaptive Graph Convolutional Networks

Spectral graph convolutional neural networks (CNNs) require approximation to the convolution to alleviate the computational complexity, resulting in performance loss. This paper proposes the topology adaptive graph convolutional network (TAGCN), a novel graph convolutional network defined in the vertex domain. We provide a systematic way to design a set of fixed-size learnable filters to perform convolutions on graphs. The topologies of these filters are adaptive to the topology of the graph when they scan the graph to perform convolution. The TAGCN not only inherits the properties of convolutions in CNN for grid-structured data, but it is also consistent with convolution as defined in graph signal processing. Since no approximation to the convolution is needed, TAGCN exhibits better performance than existing spectral CNNs on a number of data sets and is also computationally simpler than other recent methods.

Graphical Models as Block-Tree Graphs

We introduce block-tree graphs as a framework for deriving efficient algorithms on graphical models. We define block-tree graphs as a tree-structured graph where each node is a cluster of nodes such that the clusters in the graph are disjoint. This differs from junction-trees, where two clusters connected by an edge always have at least one common node. When compared to junction-trees, we show that constructing block-tree graphs is faster, and finding optimal block-tree graphs has a much smaller search space. Applying our block-tree graph framework to graphical models, we show that, for some graphs, e.g., grid graphs, using block-tree graphs for inference is computationally more efficient than using junction-trees. For graphical models with boundary conditions, the block-tree graph framework transforms the boundary valued problem into an initial value problem. For Gaussian graphical models, the block-tree graph framework leads to a linear state-space representation. Since exact inference in graphical models can be computationally intractable, we propose to use spanning block-trees to derive approximate inference algorithms. Experimental results show the improved performance in using spanning block-trees versus using spanning trees for approximate estimation over Gaussian graphical models.

Kalman Filtering with Intermittent Observations: Weak Convergence to a Stationary Distribution

The paper studies the asymptotic behavior of Random Algebraic Riccati Equations (RARE) arising in Kalman filtering when the arrival of the observations is described by a Bernoulli i.i.d. process. We model the RARE as an order-preserving, strongly sublinear random dynamical system (RDS). Under a sufficient condition, stochastic boundedness, and using a limit-set dichotomy result for order-preserving, strongly sublinear RDS, we establish the asymptotic properties of the RARE: the sequence of random prediction error covariance matrices converges weakly to a unique invariant distribution, whose support exhibits fractal behavior. In particular, this weak convergence holds under broad conditions and even when the observations arrival rate is below the critical probability for mean stability. We apply the weak-Feller property of the Markov process governing the RARE to characterize the support of the limiting invariant distribution as the topological closure of a countable set of points, which, in general, is not dense in the set of positive semi-definite matrices. We use the explicit characterization of the support of the invariant distribution and the almost sure ergodicity of the sample paths to easily compute the moments of the invariant distribution. A one dimensional example illustrates that the support is a fractured subset of the non-negative reals with self-similarity properties.