Graph Signal Processing: A Signal Representation Approach to Convolution and Sampling

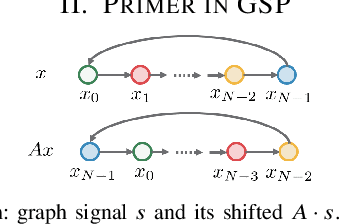
The paper presents sampling in GSP as 1) linear operations (change of bases) between signal representations and 2) downsampling as linear shift invariant filtering and reconstruction (interpolation) as filtering, both in the spectral domain. To achieve this, it considers a spectral shift $M$ that leads to a spectral graph signal processing theory, $\text{GSP}_{\textrm{sp}}$, dual to GSP but that starts from the spectral domain and $M$. The paper introduces alternative signal representations, convolution of graph signals for these alternative representations, presenting a $\textit{fast}$ GSP convolution that uses the DSP FFT algorithm, and sampling as solutions of algebraic linear systems of equations.