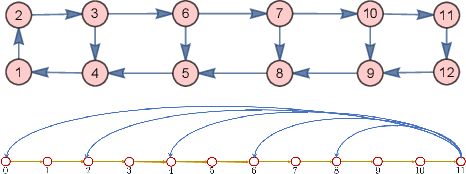
GSP = DSP + Boundary Conditions -- The Graph Signal Processing Companion Model

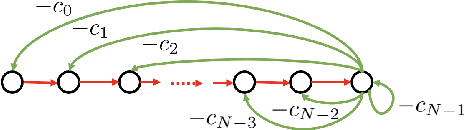
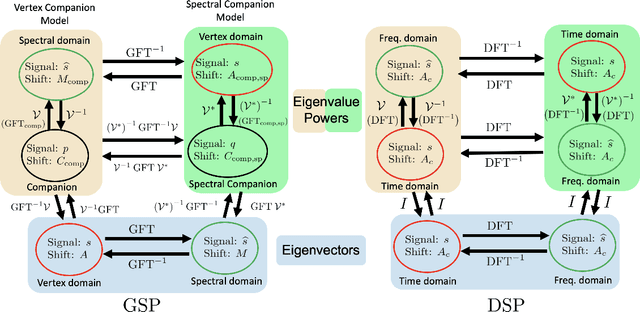
The paper presents the graph signal processing (GSP) companion model that naturally replicates the basic tenets of classical signal processing (DSP) for GSP. The companion model shows that GSP can be made equivalent to DSP 'plus' appropriate boundary conditions (bc) - this is shown under broad conditions and holds for arbitrary undirected or directed graphs. This equivalence suggests how to broaden GSP - extend naturally a DSP concept to the GSP companion model and then transfer it back to the common graph vertex and graph Fourier domains. The paper shows that GSP unrolls as two distinct models that coincide in DSP, the companion model based on (Hadamard or pointwise) powers of what we will introduce as the spectral frequency vector $\lambda$, and the traditional graph vertex model, based on the adjacency matrix and its eigenvectors. The paper expands GSP in several directions, including showing that convolution in the graph companion model can be achieved with the FFT and that GSP modulation with appropriate choice of carriers exhibits the DSP translation effect that enables multiplexing by modulation of graph signals.

The Companion Model -- a Canonical Model in Graph Signal Processing

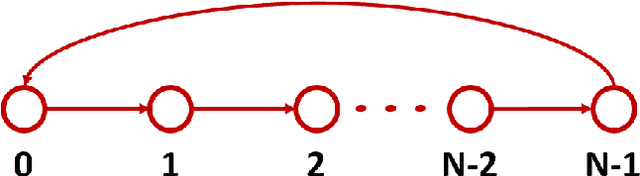
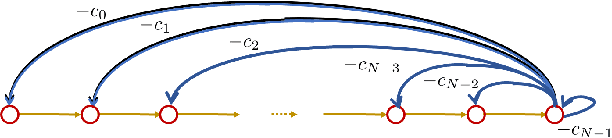
This paper introduces a $\textit{canonical}$ graph signal model defined by a $\textit{canonical}$ graph and a $\textit{canonical}$ shift, the $\textit{companion}$ graph and the $\textit{companion}$ shift. These are canonical because, under standard conditions, we show that any graph signal processing (GSP) model can be transformed into the canonical model. The transform that obtains this is the graph $z$-transform ($\textrm{G$z$T}$) that we introduce. The GSP canonical model comes closest to the discrete signal processing (DSP) time signal models: the structure of the companion shift decomposes into a line shift and a signal continuation just like the DSP shift and the GSP canonical graph is a directed line graph with a terminal condition reflecting the signal continuation condition. We further show that, surprisingly, in the canonical model, convolution of graph signals is fast convolution by the DSP FFT.

Graph Signal Processing: A Signal Representation Approach to Convolution and Sampling

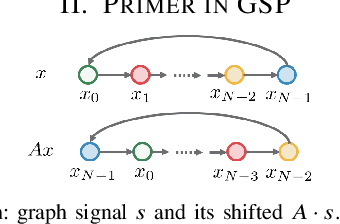
The paper presents sampling in GSP as 1) linear operations (change of bases) between signal representations and 2) downsampling as linear shift invariant filtering and reconstruction (interpolation) as filtering, both in the spectral domain. To achieve this, it considers a spectral shift $M$ that leads to a spectral graph signal processing theory, $\text{GSP}_{\textrm{sp}}$, dual to GSP but that starts from the spectral domain and $M$. The paper introduces alternative signal representations, convolution of graph signals for these alternative representations, presenting a $\textit{fast}$ GSP convolution that uses the DSP FFT algorithm, and sampling as solutions of algebraic linear systems of equations.

Edge Entropy as an Indicator of the Effectiveness of GNNs over CNNs for Node Classification

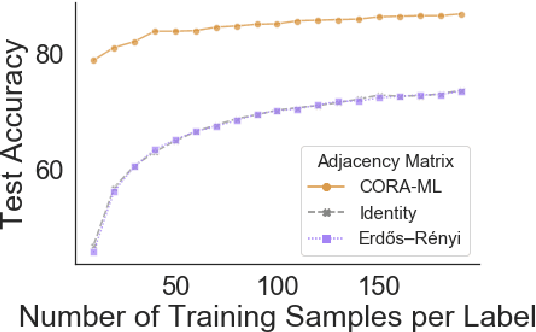
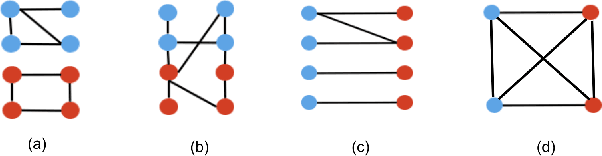
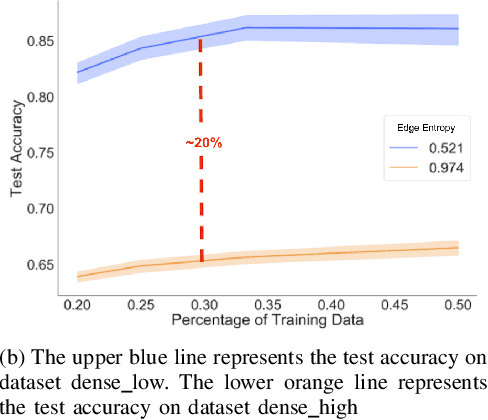
Graph neural networks (GNNs) extend convolutional neural networks (CNNs) to graph-based data. A question that arises is how much performance improvement does the underlying graph structure in the GNN provide over the CNN (that ignores this graph structure). To address this question, we introduce edge entropy and evaluate how good an indicator it is for possible performance improvement of GNNs over CNNs. Our results on node classification with synthetic and real datasets show that lower values of edge entropy predict larger expected performance gains of GNNs over CNNs, and, conversely, higher edge entropy leads to expected smaller improvement gains.

Pooling in Graph Convolutional Neural Networks

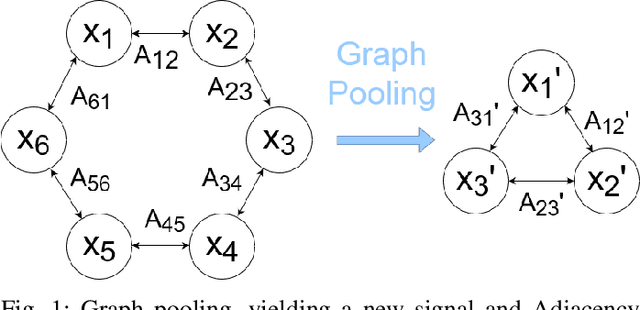
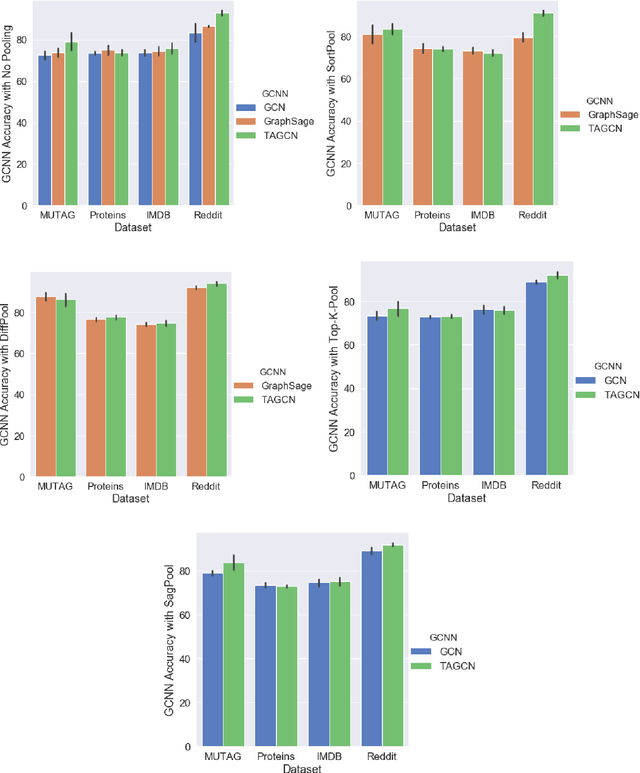
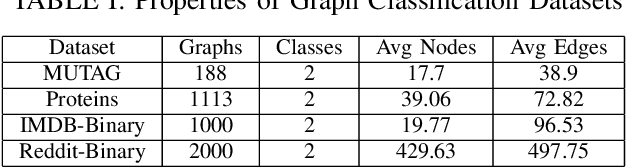
Graph convolutional neural networks (GCNNs) are a powerful extension of deep learning techniques to graph-structured data problems. We empirically evaluate several pooling methods for GCNNs, and combinations of those graph pooling methods with three different architectures: GCN, TAGCN, and GraphSAGE. We confirm that graph pooling, especially DiffPool, improves classification accuracy on popular graph classification datasets and find that, on average, TAGCN achieves comparable or better accuracy than GCN and GraphSAGE, particularly for datasets with larger and sparser graph structures.