The Companion Model -- a Canonical Model in Graph Signal Processing
Paper and Code
Mar 25, 2022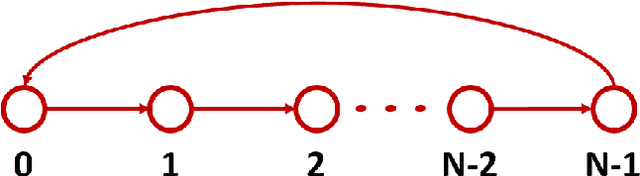
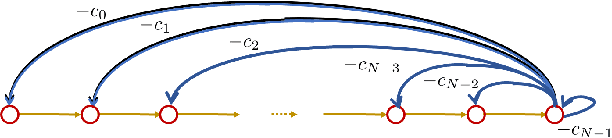

This paper introduces a $\textit{canonical}$ graph signal model defined by a $\textit{canonical}$ graph and a $\textit{canonical}$ shift, the $\textit{companion}$ graph and the $\textit{companion}$ shift. These are canonical because, under standard conditions, we show that any graph signal processing (GSP) model can be transformed into the canonical model. The transform that obtains this is the graph $z$-transform ($\textrm{G$z$T}$) that we introduce. The GSP canonical model comes closest to the discrete signal processing (DSP) time signal models: the structure of the companion shift decomposes into a line shift and a signal continuation just like the DSP shift and the GSP canonical graph is a directed line graph with a terminal condition reflecting the signal continuation condition. We further show that, surprisingly, in the canonical model, convolution of graph signals is fast convolution by the DSP FFT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge