GSP = DSP + Boundary Conditions -- The Graph Signal Processing Companion Model
Paper and Code
Mar 04, 2023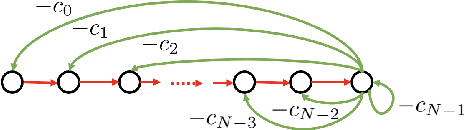
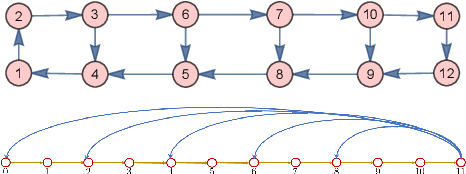
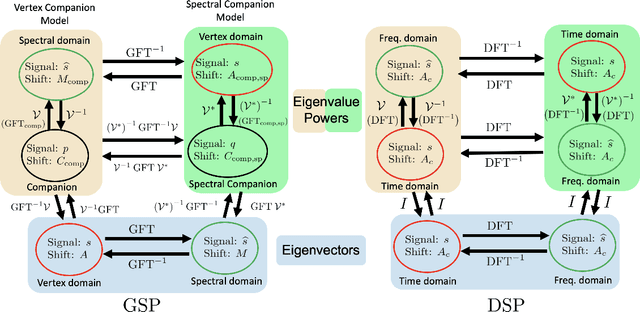
The paper presents the graph signal processing (GSP) companion model that naturally replicates the basic tenets of classical signal processing (DSP) for GSP. The companion model shows that GSP can be made equivalent to DSP 'plus' appropriate boundary conditions (bc) - this is shown under broad conditions and holds for arbitrary undirected or directed graphs. This equivalence suggests how to broaden GSP - extend naturally a DSP concept to the GSP companion model and then transfer it back to the common graph vertex and graph Fourier domains. The paper shows that GSP unrolls as two distinct models that coincide in DSP, the companion model based on (Hadamard or pointwise) powers of what we will introduce as the spectral frequency vector $\lambda$, and the traditional graph vertex model, based on the adjacency matrix and its eigenvectors. The paper expands GSP in several directions, including showing that convolution in the graph companion model can be achieved with the FFT and that GSP modulation with appropriate choice of carriers exhibits the DSP translation effect that enables multiplexing by modulation of graph signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge