Is Pontryagin's Maximum Principle all you need? Solving optimal control problems with PMP-inspired neural networks
Paper and Code
Oct 08, 2024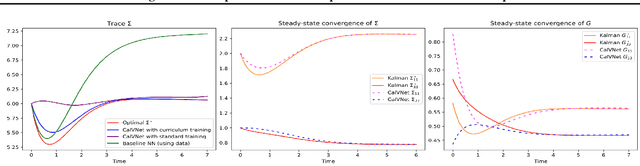

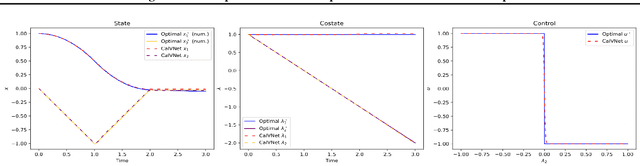
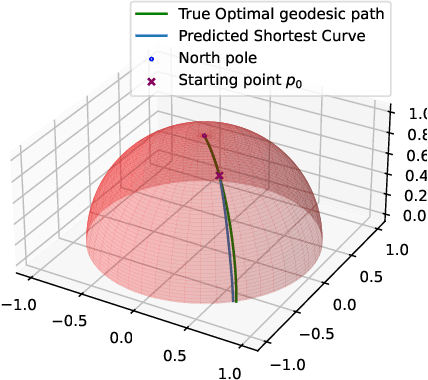
Calculus of Variations is the mathematics of functional optimization, i.e., when the solutions are functions over a time interval. This is particularly important when the time interval is unknown like in minimum-time control problems, so that forward in time solutions are not possible. Calculus of Variations offers a robust framework for learning optimal control and inference. How can this framework be leveraged to design neural networks to solve challenges in control and inference? We propose the Pontryagin's Maximum Principle Neural Network (PMP-net) that is tailored to estimate control and inference solutions, in accordance with the necessary conditions outlined by Pontryagin's Maximum Principle. We assess PMP-net on two classic optimal control and inference problems: optimal linear filtering and minimum-time control. Our findings indicate that PMP-net can be effectively trained in an unsupervised manner to solve these problems without the need for ground-truth data, successfully deriving the classical "Kalman filter" and "bang-bang" control solution. This establishes a new approach for addressing general, possibly yet unsolved, optimal control problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge