A general locomotion control framework for serially connected multi-legged robots

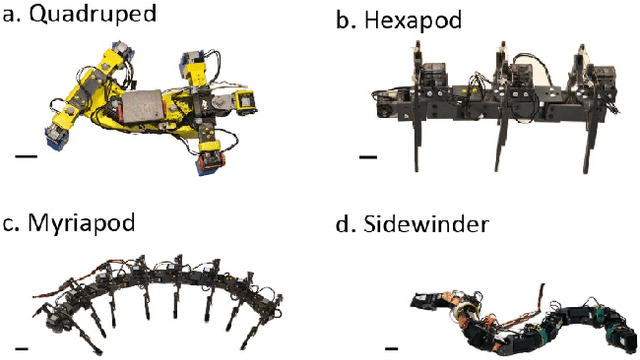
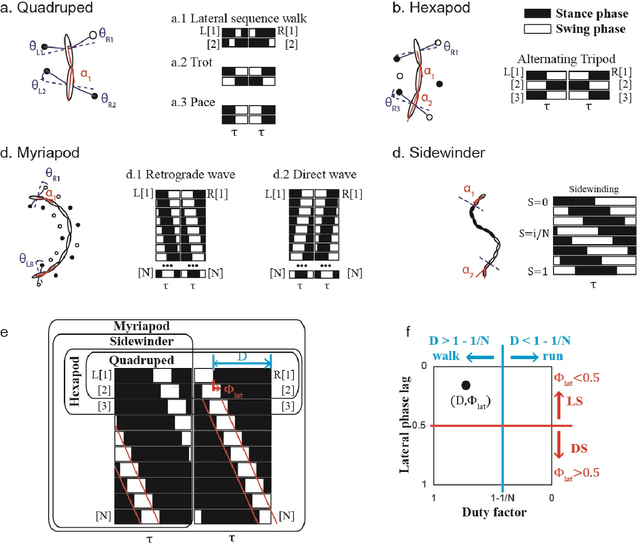
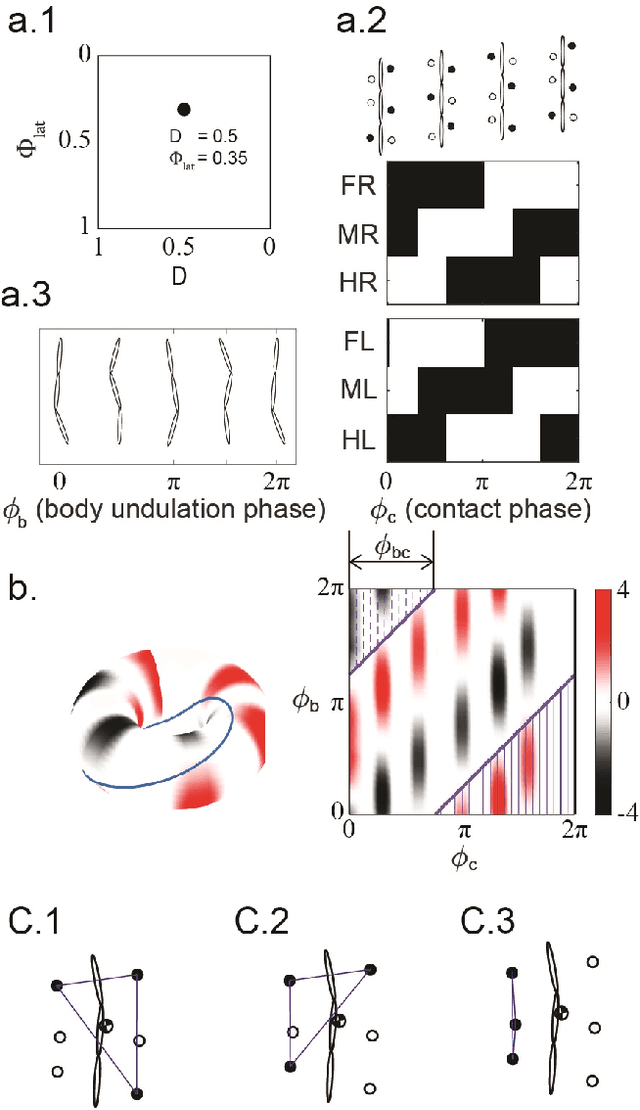
Serially connected robots are promising candidates for performing tasks in confined spaces such as search-and-rescue in large-scale disasters. Such robots are typically limbless, and we hypothesize that the addition of limbs could improve mobility. However, a challenge in designing and controlling such devices lies in the coordination of high-dimensional redundant modules in a way that improves mobility. Here we develop a general framework to control serially connected multi-legged robots. Specifically, we combine two approaches to build a general shape control scheme which can provide baseline patterns of self-deformation ("gaits") for effective locomotion in diverse robot morphologies. First, we take inspiration from a dimensionality reduction and a biological gait classification scheme to generate cyclic patterns of body deformation and foot lifting/lowering, which facilitate generation of arbitrary substrate contact patterns. Second, we use geometric mechanics methods to facilitates identification of optimal phasing of these undulations to maximize speed and/or stability. Our scheme allows the development of effective gaits in multi-legged robots locomoting on flat frictional terrain with diverse number of limbs (4, 6, 16, and even 0 limbs) and body actuation capabilities (including sidewinding gaits on limbless devices). By properly coordinating the body undulation and the leg placement, our framework combines the advantages of both limbless robots (modularity) and legged robots (mobility). We expect that our framework can provide general control schemes for the rapid deployment of general multi-legged robots, paving the ways toward machines that can traverse complex environments under real-life conditions.

Self-propulsion on spandex: toward a robotic analog gravity system

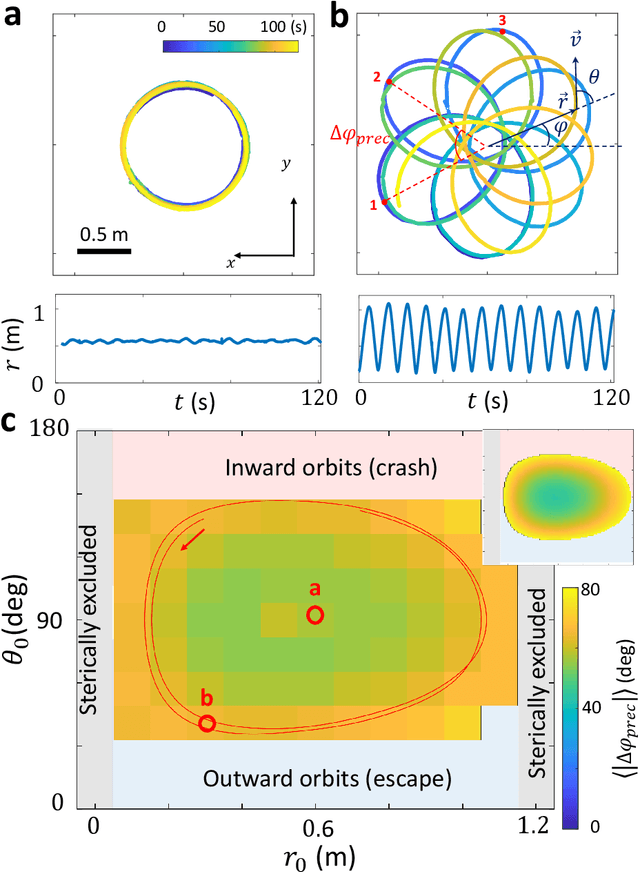
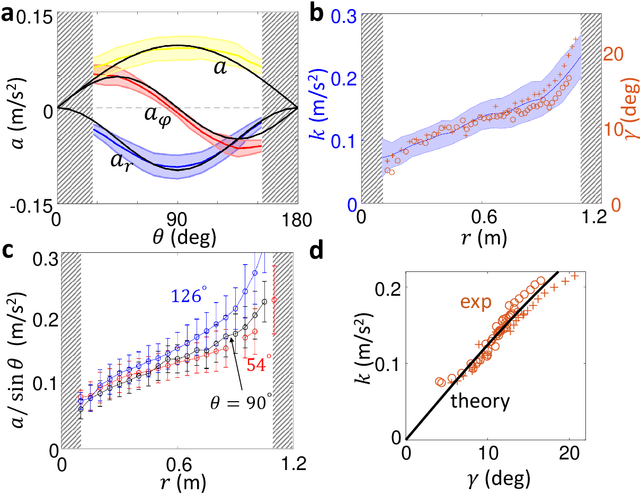
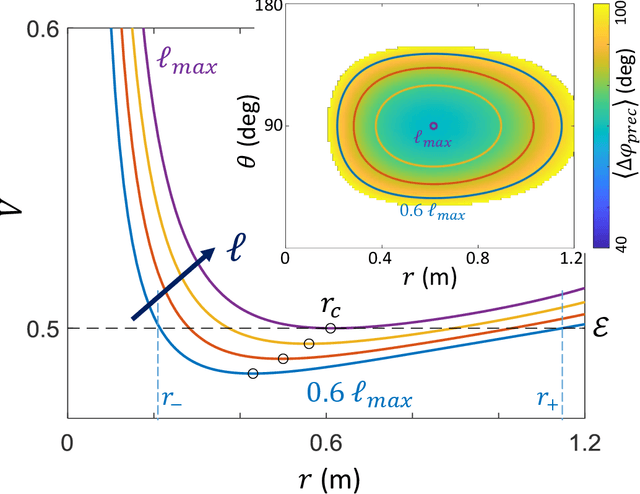
Numerous laboratory systems have been proposed as analogs to study phenomena (like black holes, Hawking radiation) associated with Einstein's theory of General Relativity (GR) but which are challenging to study in experimental or simulated astrophysical settings. Such analogs, typically acoustic, fluid, or atomic systems require delicate manipulation. Here we introduce a robotic system that captures aspects of Einstein-like dynamics in curved spacetime and creates a path toward a mechatronic analog gravity system. The system consists of a wheeled robotic vehicle transiting a deformable elastic membrane. With a fixed central depression in the membrane (mimicking a massive body), the vehicle paths around the depression resemble the dynamics observed near general-relativistic compact objects (e.g. black holes). We recast the vehicle plus membrane dynamics in physical space into geodesic motion of a so-called "test particle" in a fiducial curved space-time. The mapping facilitates understanding of how vehicle characteristics (e.g. mass) can be modified to change precession dynamics. Since an important aspect of GR is the coupling of matter and spacetime (which influence each other) we also study the dynamics of a two-robot system interacting solely via local membrane deformations. For a range of masses, we observe vehicle "attraction"; initially separated robots converge and collide. A control scheme in which a robot senses its local tilt angle and adjusts its speed enables it to escape capture. Our system provides a path towards a readily tunable analog gravity system and can aid design and control of locomoting devices (e.g. water walkers) that couple strongly to their environments.

The dynamics of scattering in undulatory active collisions

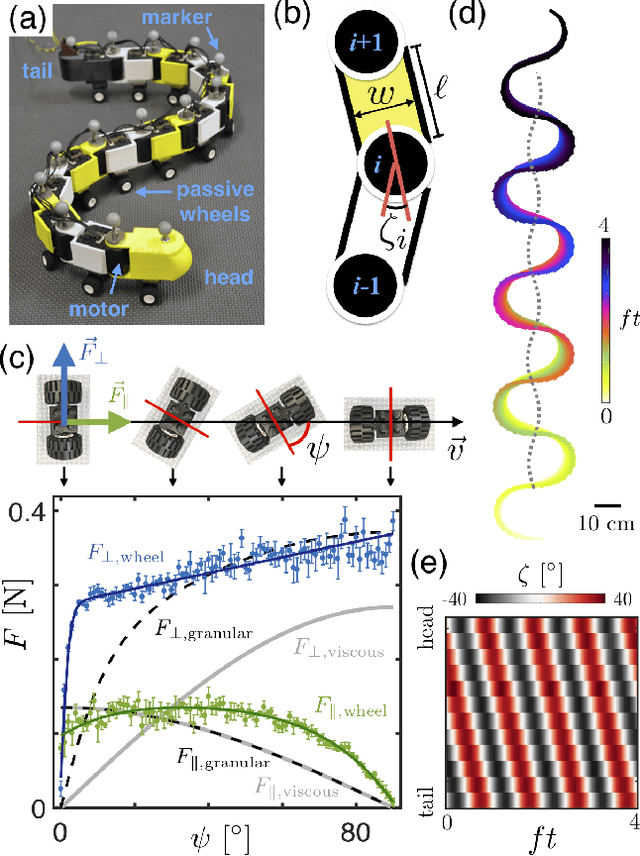
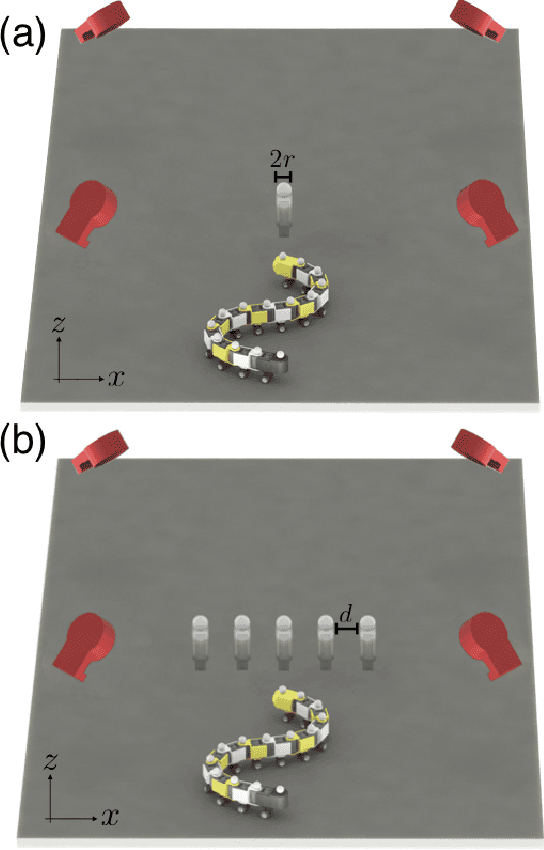
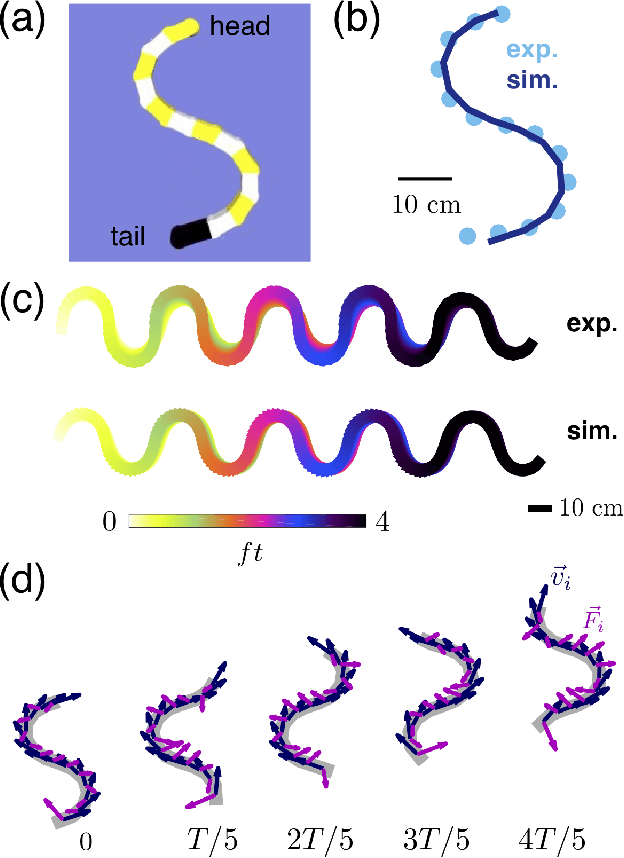
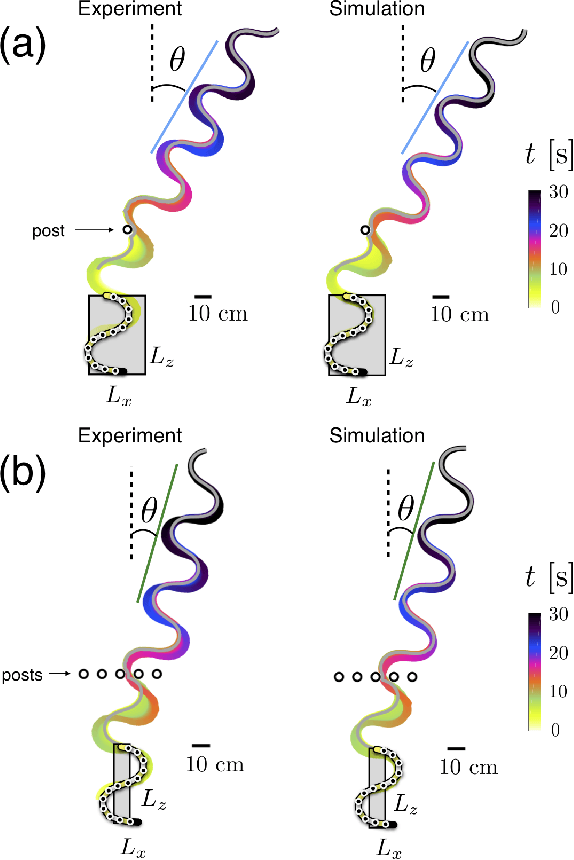
Natural and artificial self-propelled systems must manage environmental interactions during movement. Such interactions, which we refer to as active collisions, are fundamentally different from momentum-conserving interactions studied in classical physics, largely because the internal driving of the locomotor can lead to persistent contact with heterogeneities. Here, we experimentally and numerically study the effects of active collisions on a laterally-undulating sensory-deprived robophysical model, whose dynamics are applicable to self-propelled systems across length scales and environments. The robot moves via spatial undulation of body segments, with a nearly-linear center-of-geometry trajectory. Interactions with a single rigid post scatter the robot, and these deflections are proportional to the head-post contact duration. The distribution of scattering angles is smooth and strongly-peaked directly behind the post. Interactions with a single row of evenly-spaced posts (with inter-post spacing $d$) produce distributions reminiscent of far-field diffraction patterns: as $d$ decreases, distinct secondary peaks emerge as large deflections become more likely. Surprisingly, we find that the presence of multiple posts does not change the nature of individual collisions; instead, multi-modal scattering patterns arise from multiple posts altering the likelihood of individual collisions to occur. As $d$ decreases, collisions near the leading edges of the posts become more probable, and we find that these interactions are associated with larger deflections. Our results, which highlight the surprising dynamics that can occur during active collisions of self-propelled systems, can inform control principles for locomotors in complex terrain and facilitate design of task-capable active matter.