Robophysical modeling of spacetime dynamics

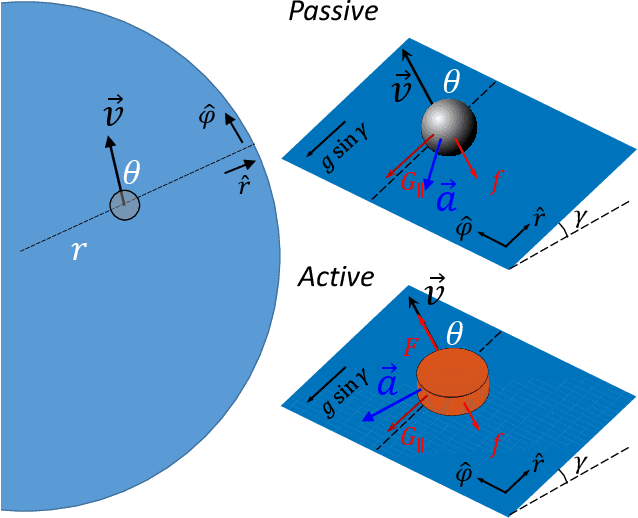
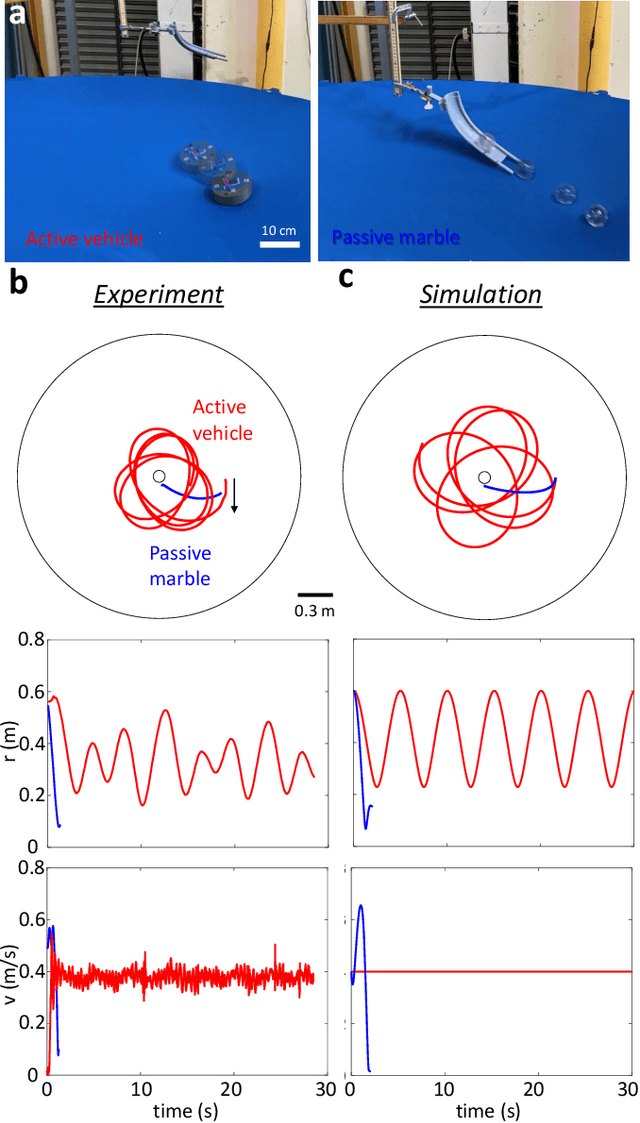
Systems consisting of spheres rolling on elastic membranes have been used as educational tools to introduce a core conceptual idea of General Relativity (GR): how curvature guides the movement of matter. However, previous studies have revealed that such schemes cannot accurately represent relativistic dynamics in the laboratory. Dissipative forces cause the initially GR-like dynamics to be transient and consequently restrict experimental study to only the beginnings of trajectories; dominance of Earth's gravity forbids the difference between spatial and temporal spacetime curvatures. Here by developing a mapping between dynamics of a wheeled vehicle on a spandex membrane, we demonstrate that an active object that can prescribe its speed can not only obtain steady-state orbits, but also use the additional parameters such as speed to tune the orbits towards relativistic dynamics. Our mapping demonstrates how activity mixes space and time in a metric, shows how active particles do not necessarily follow geodesics in the real space but instead follow geodesics in a fiducial spacetime. The mapping further reveals how parameters such as the membrane elasticity and instantaneous speed allow programming a desired spacetime such as the Schwarzschild metric near a non-rotating black hole. Our mapping and framework point the way to the possibility to create a robophysical analog gravity system in the laboratory at low cost and provide insights into active matter in deformable environments and robot exploration in complex landscapes.

ECG Beat Representation and Delineation by means of Variable Projection

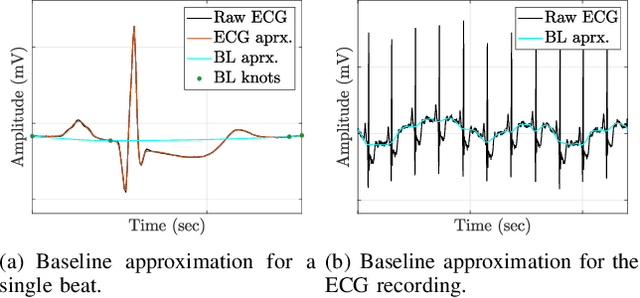
The electrocardiogram (ECG) follows a characteristic shape, which has led to the development of several mathematical models for extracting clinically important information. Our main objective is to resolve limitations of previous approaches, that means to simultaneously cope with various noise sources, perform exact beat segmentation, and to retain diagnostically important morphological information. Methods: We therefore propose a model that is based on Hermite and sigmoid functions combined with piecewise polynomial interpolation for exact segmentation and low-dimensional representation of individual ECG beat segments. Hermite and sigmoidal functions enable reliable extraction of important ECG waveform information while the piecewise polynomial interpolation captures noisy signal features like the BLW. For that we use variable projection, which allows the separation of linear and nonlinear morphological variations of the according ECG waveforms. The resulting ECG model simultaneously performs BLW cancellation, beat segmentation, and low-dimensional waveform representation. Results: We demonstrate its BLW denoising and segmentation performance in two experiments, using synthetic and real data (Physionet QT database). Compared to state-of-the-art algorithms, the experiments showed less diagnostic distortion in case of denoising and a more robust delineation for the P and T wave. Conclusion: This work suggests a novel concept for ECG beat representation, easily adaptable to other biomedical signals with similar shape characteristics, such as blood pressure and evoked potentials. Significance: Our method is able to capture linear and nonlinear wave shape changes. Therefore, it provides a novel methodology to understand the origin of morphological variations caused, for instance, by respiration, medication, and abnormalities.

Self-propulsion on spandex: toward a robotic analog gravity system

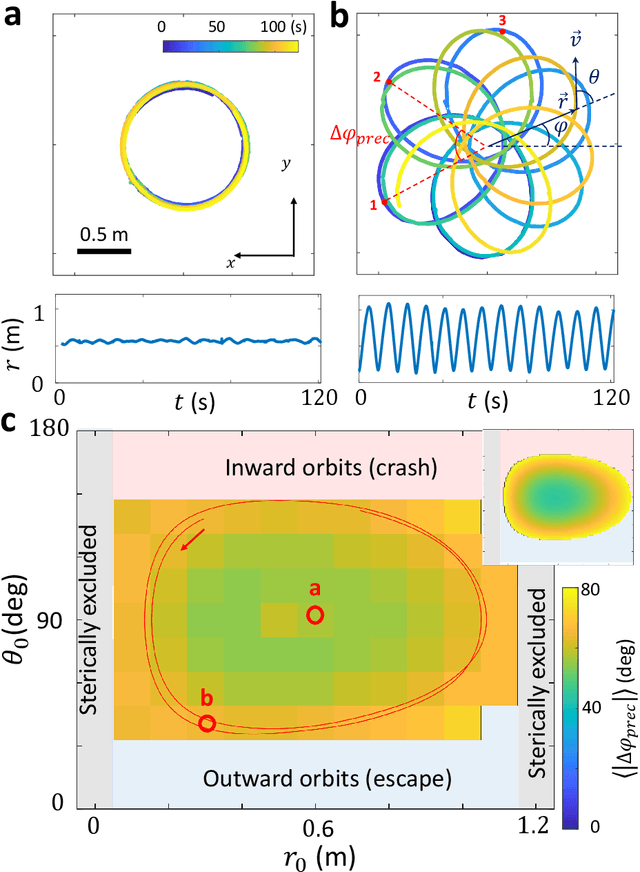
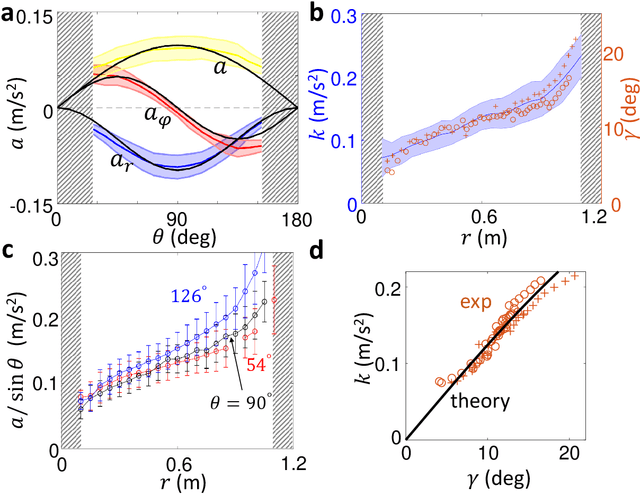
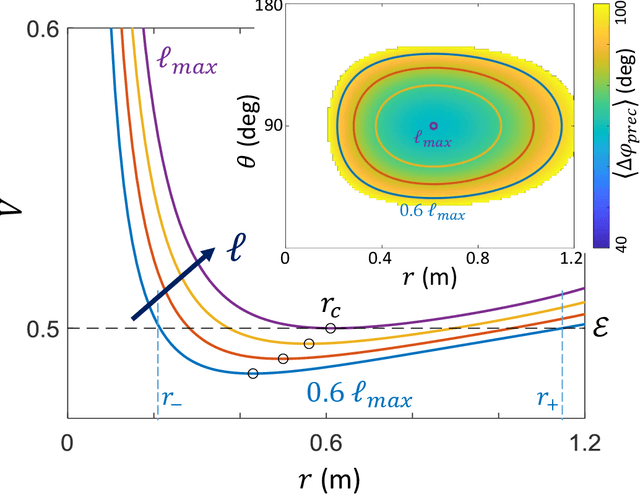
Numerous laboratory systems have been proposed as analogs to study phenomena (like black holes, Hawking radiation) associated with Einstein's theory of General Relativity (GR) but which are challenging to study in experimental or simulated astrophysical settings. Such analogs, typically acoustic, fluid, or atomic systems require delicate manipulation. Here we introduce a robotic system that captures aspects of Einstein-like dynamics in curved spacetime and creates a path toward a mechatronic analog gravity system. The system consists of a wheeled robotic vehicle transiting a deformable elastic membrane. With a fixed central depression in the membrane (mimicking a massive body), the vehicle paths around the depression resemble the dynamics observed near general-relativistic compact objects (e.g. black holes). We recast the vehicle plus membrane dynamics in physical space into geodesic motion of a so-called "test particle" in a fiducial curved space-time. The mapping facilitates understanding of how vehicle characteristics (e.g. mass) can be modified to change precession dynamics. Since an important aspect of GR is the coupling of matter and spacetime (which influence each other) we also study the dynamics of a two-robot system interacting solely via local membrane deformations. For a range of masses, we observe vehicle "attraction"; initially separated robots converge and collide. A control scheme in which a robot senses its local tilt angle and adjusts its speed enables it to escape capture. Our system provides a path towards a readily tunable analog gravity system and can aid design and control of locomoting devices (e.g. water walkers) that couple strongly to their environments.