ECG Beat Representation and Delineation by means of Variable Projection
Paper and Code
Sep 27, 2021


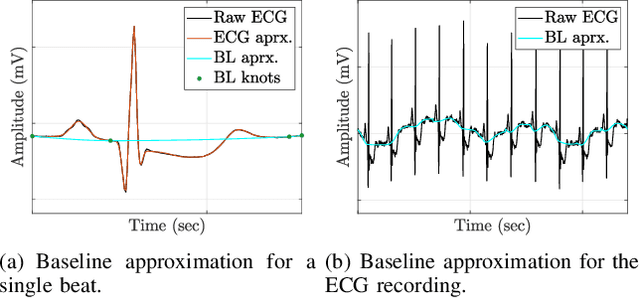
The electrocardiogram (ECG) follows a characteristic shape, which has led to the development of several mathematical models for extracting clinically important information. Our main objective is to resolve limitations of previous approaches, that means to simultaneously cope with various noise sources, perform exact beat segmentation, and to retain diagnostically important morphological information. Methods: We therefore propose a model that is based on Hermite and sigmoid functions combined with piecewise polynomial interpolation for exact segmentation and low-dimensional representation of individual ECG beat segments. Hermite and sigmoidal functions enable reliable extraction of important ECG waveform information while the piecewise polynomial interpolation captures noisy signal features like the BLW. For that we use variable projection, which allows the separation of linear and nonlinear morphological variations of the according ECG waveforms. The resulting ECG model simultaneously performs BLW cancellation, beat segmentation, and low-dimensional waveform representation. Results: We demonstrate its BLW denoising and segmentation performance in two experiments, using synthetic and real data (Physionet QT database). Compared to state-of-the-art algorithms, the experiments showed less diagnostic distortion in case of denoising and a more robust delineation for the P and T wave. Conclusion: This work suggests a novel concept for ECG beat representation, easily adaptable to other biomedical signals with similar shape characteristics, such as blood pressure and evoked potentials. Significance: Our method is able to capture linear and nonlinear wave shape changes. Therefore, it provides a novel methodology to understand the origin of morphological variations caused, for instance, by respiration, medication, and abnormalities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge