Search-Based Correction of Reasoning Chains for Language Models

Chain-of-Thought (CoT) reasoning has advanced the capabilities and transparency of language models (LMs); however, reasoning chains can contain inaccurate statements that reduce performance and trustworthiness. To address this, we introduce a new self-correction framework that augments each reasoning step in a CoT with a latent variable indicating its veracity, enabling modeling of all possible truth assignments rather than assuming correctness throughout. To efficiently explore this expanded space, we introduce Search Corrector, a discrete search algorithm over boolean-valued veracity assignments. It efficiently performs otherwise intractable inference in the posterior distribution over veracity assignments by leveraging the LM's joint likelihood over veracity and the final answer as a proxy reward. This efficient inference-time correction method facilitates supervised fine-tuning of an Amortized Corrector by providing pseudo-labels for veracity. The Amortized Corrector generalizes self-correction, enabling accurate zero-shot veracity inference in novel contexts. Empirical results demonstrate that Search Corrector reliably identifies errors in logical (ProntoQA) and mathematical reasoning (GSM8K) benchmarks. The Amortized Corrector achieves comparable zero-shot accuracy and improves final answer accuracy by up to 25%.

Probabilistic Temporal Prediction of Continuous Disease Trajectories and Treatment Effects Using Neural SDEs

Personalized medicine based on medical images, including predicting future individualized clinical disease progression and treatment response, would have an enormous impact on healthcare and drug development, particularly for diseases (e.g. multiple sclerosis (MS)) with long term, complex, heterogeneous evolutions and no cure. In this work, we present the first stochastic causal temporal framework to model the continuous temporal evolution of disease progression via Neural Stochastic Differential Equations (NSDE). The proposed causal inference model takes as input the patient's high dimensional images (MRI) and tabular data, and predicts both factual and counterfactual progression trajectories on different treatments in latent space. The NSDE permits the estimation of high-confidence personalized trajectories and treatment effects. Extensive experiments were performed on a large, multi-centre, proprietary dataset of patient 3D MRI and clinical data acquired during several randomized clinical trials for MS treatments. Our results present the first successful uncertainty-based causal Deep Learning (DL) model to: (a) accurately predict future patient MS disability evolution (e.g. EDSS) and treatment effects leveraging baseline MRI, and (b) permit the discovery of subgroups of patients for which the model has high confidence in their response to treatment even in clinical trials which did not reach their clinical endpoints.

Delta-AI: Local objectives for amortized inference in sparse graphical models

We present a new algorithm for amortized inference in sparse probabilistic graphical models (PGMs), which we call $\Delta$-amortized inference ($\Delta$-AI). Our approach is based on the observation that when the sampling of variables in a PGM is seen as a sequence of actions taken by an agent, sparsity of the PGM enables local credit assignment in the agent's policy learning objective. This yields a local constraint that can be turned into a local loss in the style of generative flow networks (GFlowNets) that enables off-policy training but avoids the need to instantiate all the random variables for each parameter update, thus speeding up training considerably. The $\Delta$-AI objective matches the conditional distribution of a variable given its Markov blanket in a tractable learned sampler, which has the structure of a Bayesian network, with the same conditional distribution under the target PGM. As such, the trained sampler recovers marginals and conditional distributions of interest and enables inference of partial subsets of variables. We illustrate $\Delta$-AI's effectiveness for sampling from synthetic PGMs and training latent variable models with sparse factor structure.

Improving Image-Based Precision Medicine with Uncertainty-Aware Causal Models

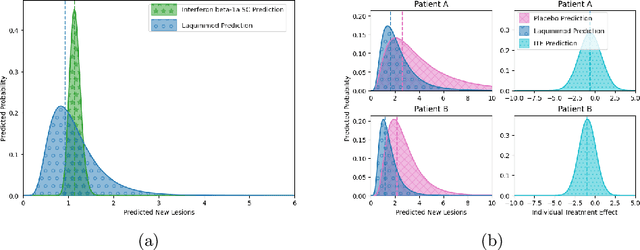
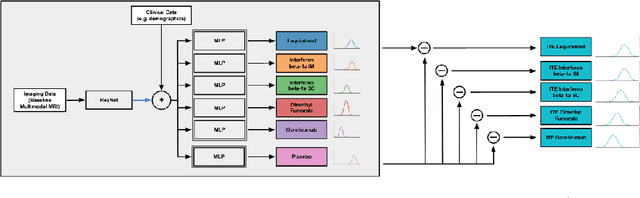
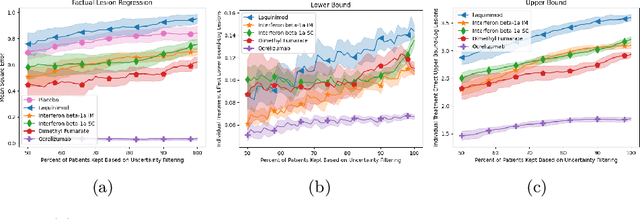
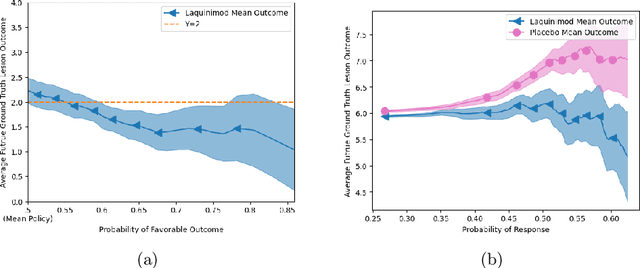
Image-based precision medicine aims to personalize treatment decisions based on an individual's unique imaging features so as to improve their clinical outcome. Machine learning frameworks that integrate uncertainty estimation as part of their treatment recommendations would be safer and more reliable. However, little work has been done in adapting uncertainty estimation techniques and validation metrics for precision medicine. In this paper, we use Bayesian deep learning for estimating the posterior distribution over factual and counterfactual outcomes on several treatments. This allows for estimating the uncertainty for each treatment option and for the individual treatment effects (ITE) between any two treatments. We train and evaluate this model to predict future new and enlarging T2 lesion counts on a large, multi-center dataset of MR brain images of patients with multiple sclerosis, exposed to several treatments during randomized controlled trials. We evaluate the correlation of the uncertainty estimate with the factual error, and, given the lack of ground truth counterfactual outcomes, demonstrate how uncertainty for the ITE prediction relates to bounds on the ITE error. Lastly, we demonstrate how knowledge of uncertainty could modify clinical decision-making to improve individual patient and clinical trial outcomes.