Port-Hamiltonian Neural ODE Networks on Lie Groups For Robot Dynamics Learning and Control

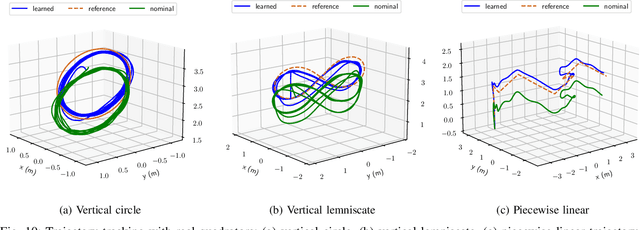
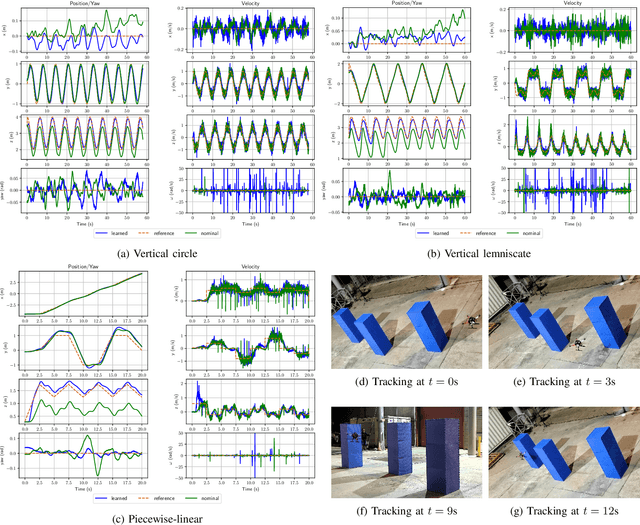
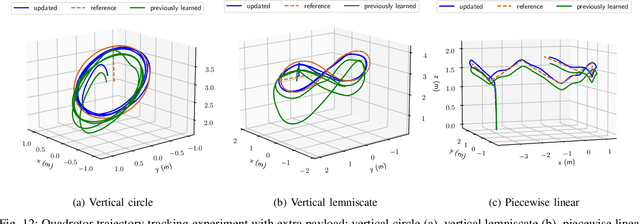
Accurate models of robot dynamics are critical for safe and stable control and generalization to novel operational conditions. Hand-designed models, however, may be insufficiently accurate, even after careful parameter tuning. This motivates the use of machine learning techniques to approximate the robot dynamics over a training set of state-control trajectories. The dynamics of many robots are described in terms of their generalized coordinates on a matrix Lie group, e.g. on SE(3) for ground, aerial, and underwater vehicles, and generalized velocity, and satisfy conservation of energy principles. This paper proposes a (port-)Hamiltonian formulation over a Lie group of the structure of a neural ordinary differential equation (ODE) network to approximate the robot dynamics. In contrast to a black-box ODE network, our formulation guarantees energy conservation principle and Lie group's constraints by construction and explicitly accounts for energy-dissipation effect such as friction and drag forces in the dynamics model. We develop energy shaping and damping injection control for the learned, potentially under-actuated Hamiltonian dynamics to enable a unified approach for stabilization and trajectory tracking with various robot platforms.

Hamiltonian Dynamics Learning from Point Cloud Observations for Nonholonomic Mobile Robot Control

Reliable autonomous navigation requires adapting the control policy of a mobile robot in response to dynamics changes in different operational conditions. Hand-designed dynamics models may struggle to capture model variations due to a limited set of parameters. Data-driven dynamics learning approaches offer higher model capacity and better generalization but require large amounts of state-labeled data. This paper develops an approach for learning robot dynamics directly from point-cloud observations, removing the need and associated errors of state estimation, while embedding Hamiltonian structure in the dynamics model to improve data efficiency. We design an observation-space loss that relates motion prediction from the dynamics model with motion prediction from point-cloud registration to train a Hamiltonian neural ordinary differential equation. The learned Hamiltonian model enables the design of an energy-shaping model-based tracking controller for rigid-body robots. We demonstrate dynamics learning and tracking control on a real nonholonomic wheeled robot.

Uncertainty as a Form of Transparency: Measuring, Communicating, and Using Uncertainty

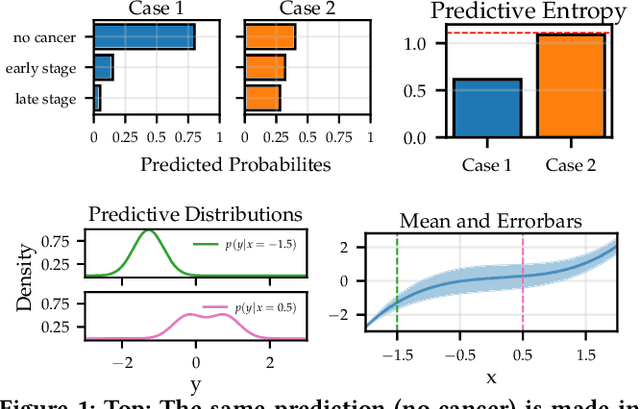
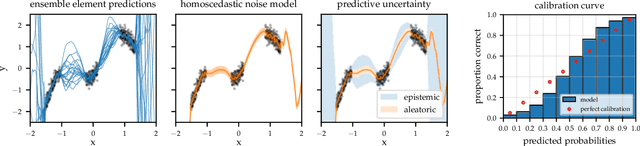
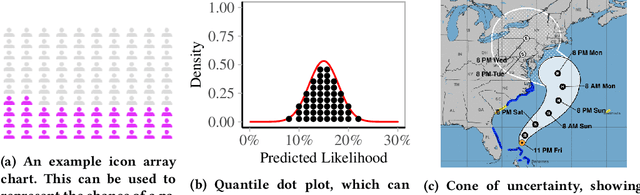
Transparency of algorithmic systems entails exposing system properties to various stakeholders for purposes that include understanding, improving, and/or contesting predictions. The machine learning (ML) community has mostly considered explainability as a proxy for transparency. With this work, we seek to encourage researchers to study uncertainty as a form of transparency and practitioners to communicate uncertainty estimates to stakeholders. First, we discuss methods for assessing uncertainty. Then, we describe the utility of uncertainty for mitigating model unfairness, augmenting decision-making, and building trustworthy systems. We also review methods for displaying uncertainty to stakeholders and discuss how to collect information required for incorporating uncertainty into existing ML pipelines. Our contribution is an interdisciplinary review to inform how to measure, communicate, and use uncertainty as a form of transparency.

Active Diagnosis via AUC Maximization: An Efficient Approach for Multiple Fault Identification in Large Scale, Noisy Networks

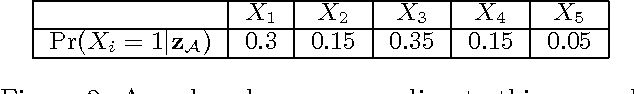
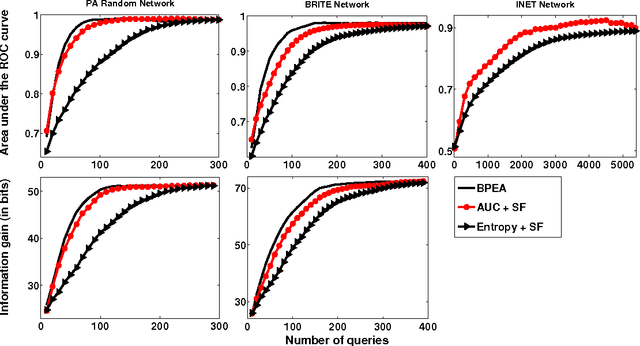
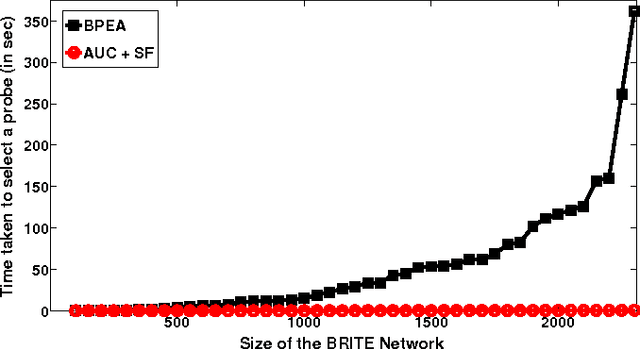
The problem of active diagnosis arises in several applications such as disease diagnosis, and fault diagnosis in computer networks, where the goal is to rapidly identify the binary states of a set of objects (e.g., faulty or working) by sequentially selecting, and observing, (noisy) responses to binary valued queries. Current algorithms in this area rely on loopy belief propagation for active query selection. These algorithms have an exponential time complexity, making them slow and even intractable in large networks. We propose a rank-based greedy algorithm that sequentially chooses queries such that the area under the ROC curve of the rank-based output is maximized. The AUC criterion allows us to make a simplifying assumption that significantly reduces the complexity of active query selection (from exponential to near quadratic), with little or no compromise on the performance quality.