Adaptive-Frequency Model Learning and Predictive Control for Dynamic Maneuvers on Legged Robots

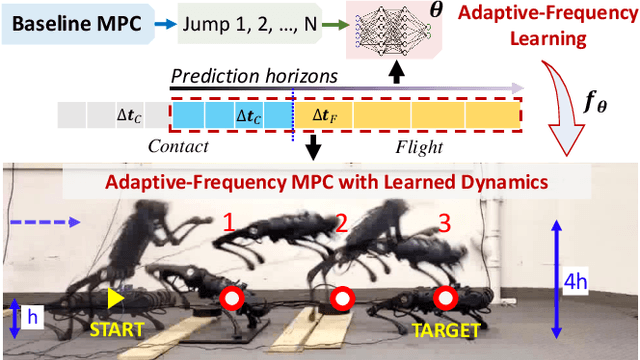
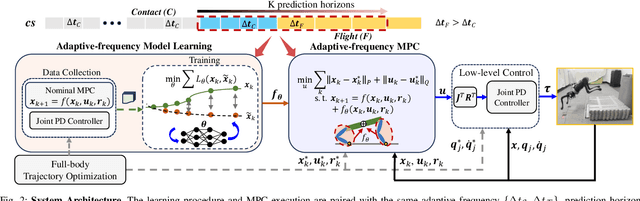
Achieving both target accuracy and robustness in dynamic maneuvers with long flight phases, such as high or long jumps, has been a significant challenge for legged robots. To address this challenge, we propose a novel learning-based control approach consisting of model learning and model predictive control (MPC) utilizing an adaptive frequency scheme. Compared to existing MPC techniques, we learn a model directly from experiments, accounting not only for leg dynamics but also for modeling errors and unknown dynamics mismatch in hardware and during contact. Additionally, learning the model with adaptive frequency allows us to cover the entire flight phase and final jumping target, enhancing the prediction accuracy of the jumping trajectory. Using the learned model, we also design an adaptive-frequency MPC to effectively leverage different jumping phases and track the target accurately. In hardware experiments with a Unitree A1 robot, we demonstrate that our approach outperforms baseline MPC using a nominal model, reducing the jumping distance error up to 8 times. We achieve jumping distance errors of less than 3 percent during continuous jumping on uneven terrain with randomly-placed perturbations of random heights (up to 4 cm or 27 percent of the robot's standing height). Our approach obtains distance errors of 1-2 cm on 34 single and continuous jumps with different jumping targets and model uncertainties.

Port-Hamiltonian Neural ODE Networks on Lie Groups For Robot Dynamics Learning and Control

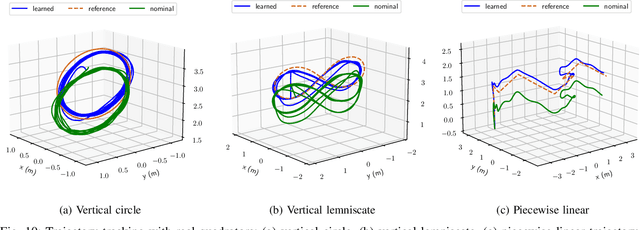
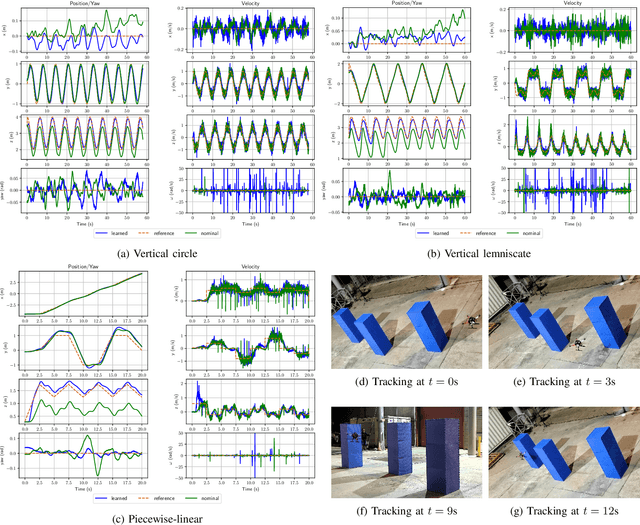
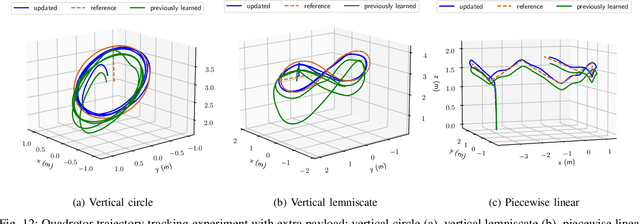
Accurate models of robot dynamics are critical for safe and stable control and generalization to novel operational conditions. Hand-designed models, however, may be insufficiently accurate, even after careful parameter tuning. This motivates the use of machine learning techniques to approximate the robot dynamics over a training set of state-control trajectories. The dynamics of many robots are described in terms of their generalized coordinates on a matrix Lie group, e.g. on SE(3) for ground, aerial, and underwater vehicles, and generalized velocity, and satisfy conservation of energy principles. This paper proposes a (port-)Hamiltonian formulation over a Lie group of the structure of a neural ordinary differential equation (ODE) network to approximate the robot dynamics. In contrast to a black-box ODE network, our formulation guarantees energy conservation principle and Lie group's constraints by construction and explicitly accounts for energy-dissipation effect such as friction and drag forces in the dynamics model. We develop energy shaping and damping injection control for the learned, potentially under-actuated Hamiltonian dynamics to enable a unified approach for stabilization and trajectory tracking with various robot platforms.

Hamiltonian Dynamics Learning from Point Cloud Observations for Nonholonomic Mobile Robot Control

Reliable autonomous navigation requires adapting the control policy of a mobile robot in response to dynamics changes in different operational conditions. Hand-designed dynamics models may struggle to capture model variations due to a limited set of parameters. Data-driven dynamics learning approaches offer higher model capacity and better generalization but require large amounts of state-labeled data. This paper develops an approach for learning robot dynamics directly from point-cloud observations, removing the need and associated errors of state estimation, while embedding Hamiltonian structure in the dynamics model to improve data efficiency. We design an observation-space loss that relates motion prediction from the dynamics model with motion prediction from point-cloud registration to train a Hamiltonian neural ordinary differential equation. The learned Hamiltonian model enables the design of an energy-shaping model-based tracking controller for rigid-body robots. We demonstrate dynamics learning and tracking control on a real nonholonomic wheeled robot.