Robust Counterfactual Explanations for Tree-Based Ensembles

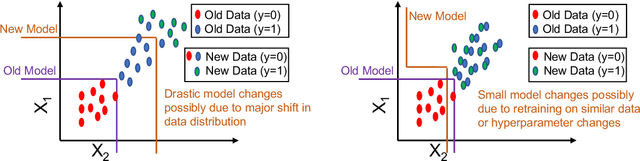
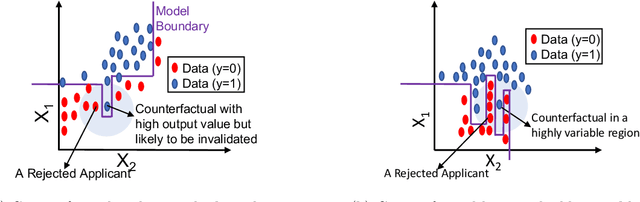
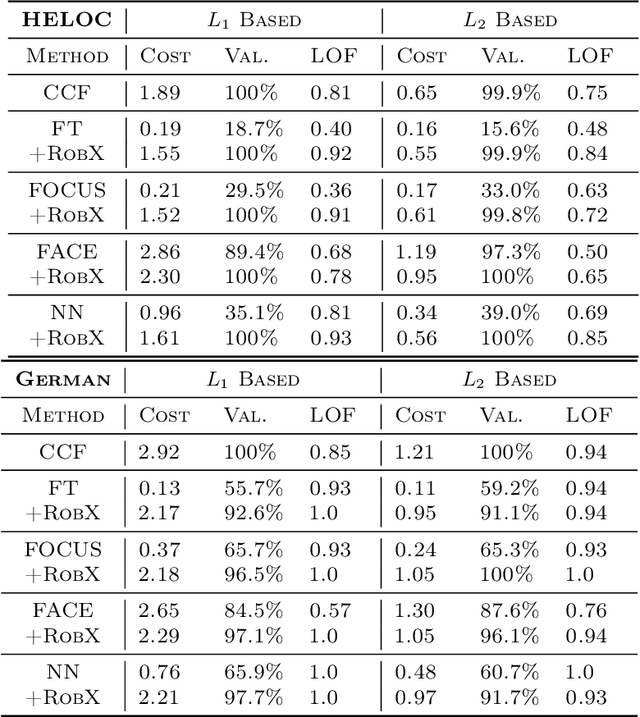
Counterfactual explanations inform ways to achieve a desired outcome from a machine learning model. However, such explanations are not robust to certain real-world changes in the underlying model (e.g., retraining the model, changing hyperparameters, etc.), questioning their reliability in several applications, e.g., credit lending. In this work, we propose a novel strategy -- that we call RobX -- to generate robust counterfactuals for tree-based ensembles, e.g., XGBoost. Tree-based ensembles pose additional challenges in robust counterfactual generation, e.g., they have a non-smooth and non-differentiable objective function, and they can change a lot in the parameter space under retraining on very similar data. We first introduce a novel metric -- that we call Counterfactual Stability -- that attempts to quantify how robust a counterfactual is going to be to model changes under retraining, and comes with desirable theoretical properties. Our proposed strategy RobX works with any counterfactual generation method (base method) and searches for robust counterfactuals by iteratively refining the counterfactual generated by the base method using our metric Counterfactual Stability. We compare the performance of RobX with popular counterfactual generation methods (for tree-based ensembles) across benchmark datasets. The results demonstrate that our strategy generates counterfactuals that are significantly more robust (nearly 100% validity after actual model changes) and also realistic (in terms of local outlier factor) over existing state-of-the-art methods.

Reductive MDPs: A Perspective Beyond Temporal Horizons

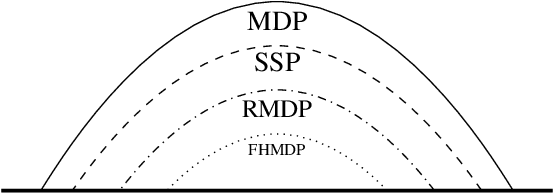
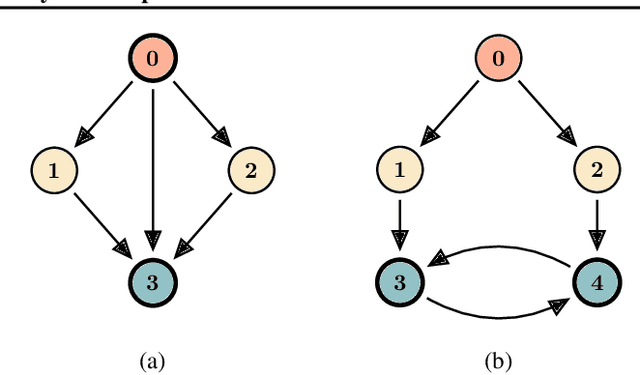
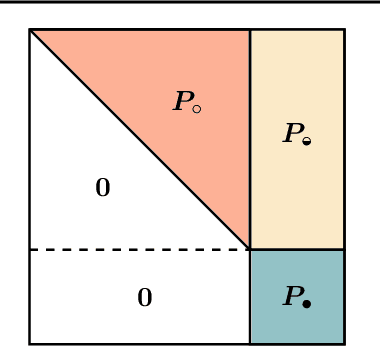
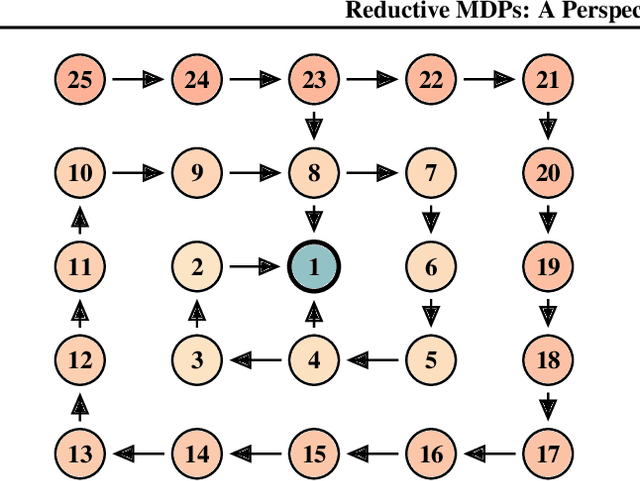
Solving general Markov decision processes (MDPs) is a computationally hard problem. Solving finite-horizon MDPs, on the other hand, is highly tractable with well known polynomial-time algorithms. What drives this extreme disparity, and do problems exist that lie between these diametrically opposed complexities? In this paper we identify and analyse a sub-class of stochastic shortest path problems (SSPs) for general state-action spaces whose dynamics satisfy a particular drift condition. This construction generalises the traditional, temporal notion of a horizon via decreasing reachability: a property called reductivity. It is shown that optimal policies can be recovered in polynomial-time for reductive SSPs -- via an extension of backwards induction -- with an efficient analogue in reductive MDPs. The practical considerations of the proposed approach are discussed, and numerical verification provided on a canonical optimal liquidation problem.

Optimal Admission Control for Multiclass Queues with Time-Varying Arrival Rates via State Abstraction

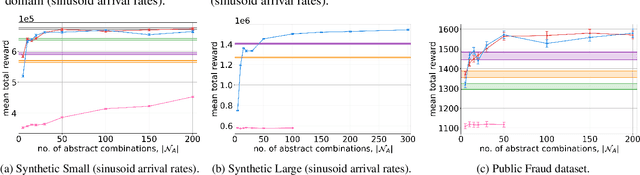
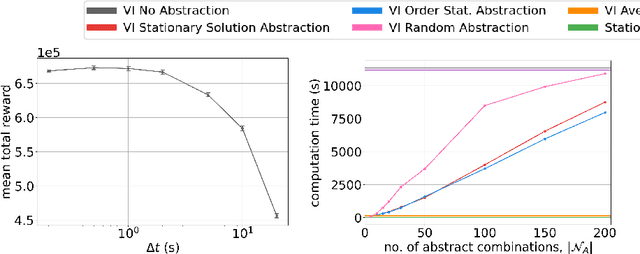
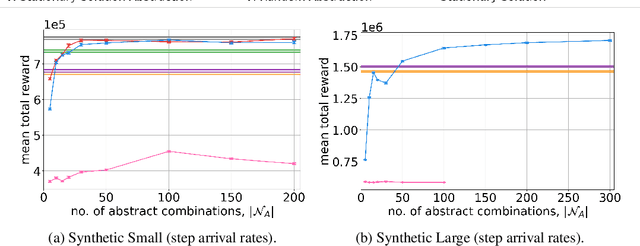
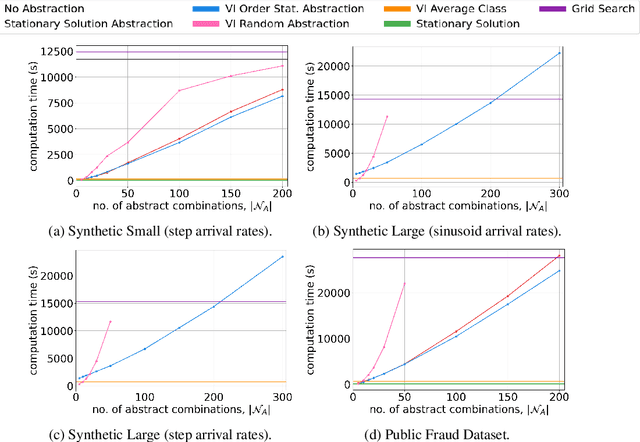
We consider a novel queuing problem where the decision-maker must choose to accept or reject randomly arriving tasks into a no buffer queue which are processed by $N$ identical servers. Each task has a price, which is a positive real number, and a class. Each class of task has a different price distribution and service rate, and arrives according to an inhomogenous Poisson process. The objective is to decide which tasks to accept so that the total price of tasks processed is maximised over a finite horizon. We formulate the problem as a discrete time Markov Decision Process (MDP) with a hybrid state space. We show that the optimal value function has a specific structure, which enables us to solve the hybrid MDP exactly. Moreover, we prove that as the time step is reduced, the discrete time solution approaches the optimal solution to the original continuous time problem. To improve the scalability of our approach to a greater number of task classes, we present an approximation based on state abstraction. We validate our approach on synthetic data, as well as a real financial fraud data set, which is the motivating application for this work.

Counterfactual Shapley Additive Explanations

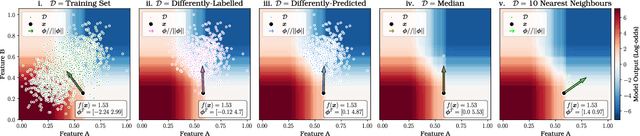
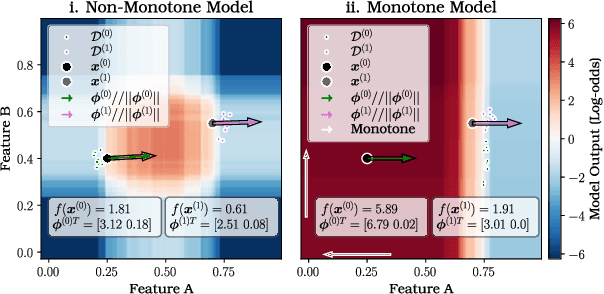
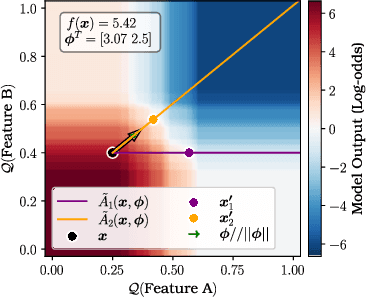
Feature attributions are a common paradigm for model explanations due to their simplicity in assigning a single numeric score for each input feature to a model. In the actionable recourse setting, wherein the goal of the explanations is to improve outcomes for model consumers, it is often unclear how feature attributions should be correctly used. With this work, we aim to strengthen and clarify the link between actionable recourse and feature attributions. Concretely, we propose a variant of SHAP, CoSHAP, that uses counterfactual generation techniques to produce a background dataset for use within the marginal (a.k.a. interventional) Shapley value framework. We motivate the need within the actionable recourse setting for careful consideration of background datasets when using Shapley values for feature attributions, alongside the requirement for monotonicity, with numerous synthetic examples. Moreover, we demonstrate the efficacy of CoSHAP by proposing and justifying a quantitative score for feature attributions, counterfactual-ability, showing that as measured by this metric, CoSHAP is superior to existing methods when evaluated on public datasets using monotone tree ensembles.

A Survey on the Robustness of Feature Importance and Counterfactual Explanations

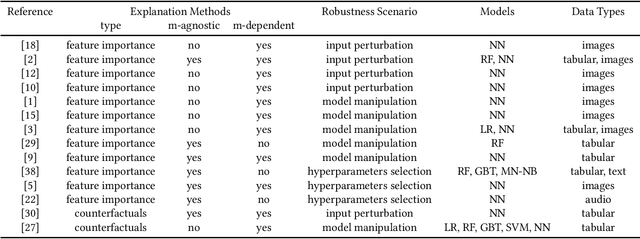
There exist several methods that aim to address the crucial task of understanding the behaviour of AI/ML models. Arguably, the most popular among them are local explanations that focus on investigating model behaviour for individual instances. Several methods have been proposed for local analysis, but relatively lesser effort has gone into understanding if the explanations are robust and accurately reflect the behaviour of underlying models. In this work, we present a survey of the works that analysed the robustness of two classes of local explanations (feature importance and counterfactual explanations) that are popularly used in analysing AI/ML models in finance. The survey aims to unify existing definitions of robustness, introduces a taxonomy to classify different robustness approaches, and discusses some interesting results. Finally, the survey introduces some pointers about extending current robustness analysis approaches so as to identify reliable explainability methods.

Counterfactual Explanations for Arbitrary Regression Models

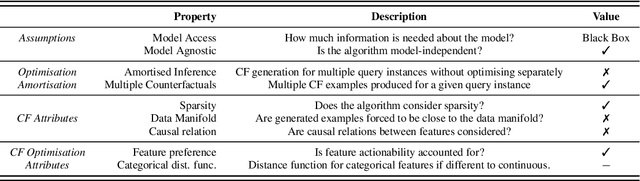
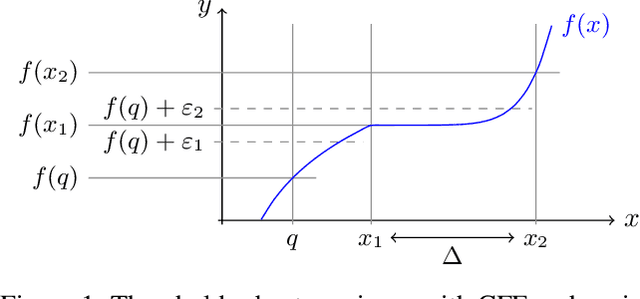
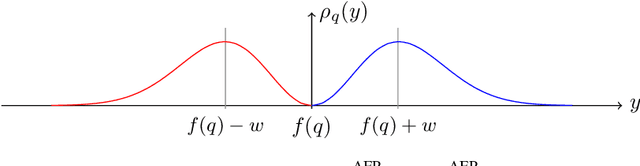
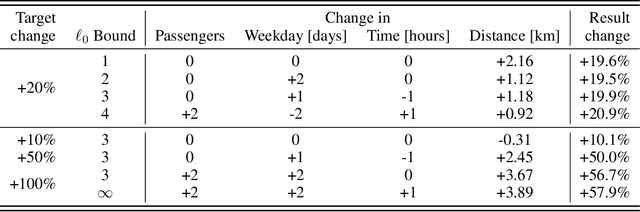
We present a new method for counterfactual explanations (CFEs) based on Bayesian optimisation that applies to both classification and regression models. Our method is a globally convergent search algorithm with support for arbitrary regression models and constraints like feature sparsity and actionable recourse, and furthermore can answer multiple counterfactual questions in parallel while learning from previous queries. We formulate CFE search for regression models in a rigorous mathematical framework using differentiable potentials, which resolves robustness issues in threshold-based objectives. We prove that in this framework, (a) verifying the existence of counterfactuals is NP-complete; and (b) that finding instances using such potentials is CLS-complete. We describe a unified algorithm for CFEs using a specialised acquisition function that composes both expected improvement and an exponential-polynomial (EP) family with desirable properties. Our evaluation on real-world benchmark domains demonstrate high sample-efficiency and precision.