Permutative redundancy and uncertainty of the objective in deep learning

Implications of uncertain objective functions and permutative symmetry of traditional deep learning architectures are discussed. It is shown that traditional architectures are polluted by an astronomical number of equivalent global and local optima. Uncertainty of the objective makes local optima unattainable, and, as the size of the network grows, the global optimization landscape likely becomes a tangled web of valleys and ridges. Some remedies which reduce or eliminate ghost optima are discussed including forced pre-pruning, re-ordering, ortho-polynomial activations, and modular bio-inspired architectures.

Reductive MDPs: A Perspective Beyond Temporal Horizons

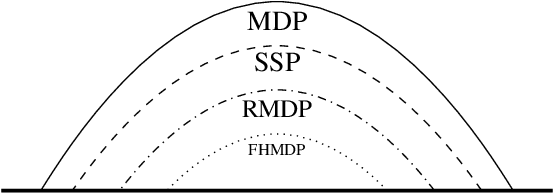
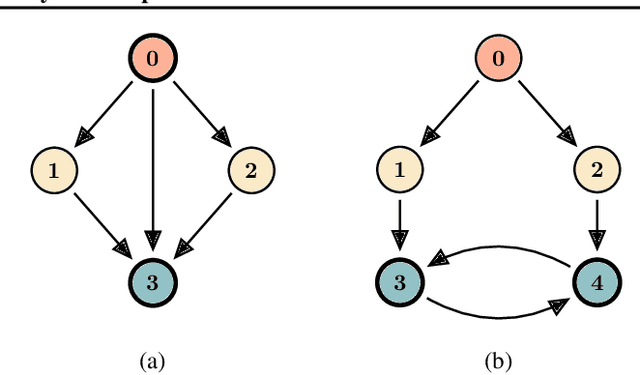
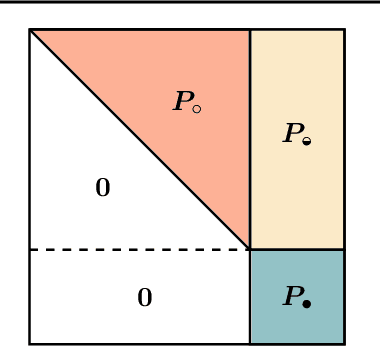
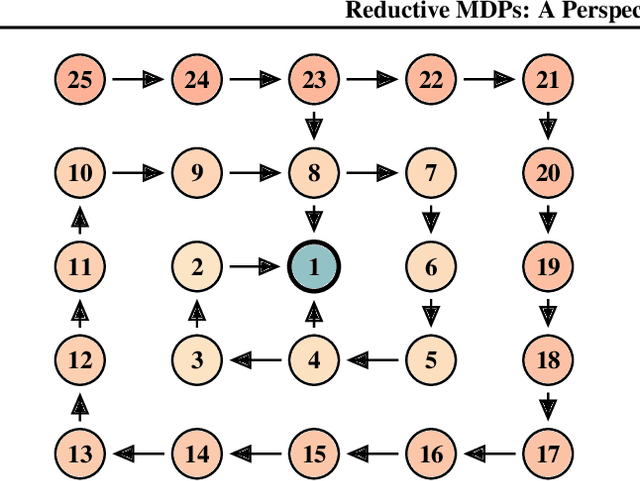
Solving general Markov decision processes (MDPs) is a computationally hard problem. Solving finite-horizon MDPs, on the other hand, is highly tractable with well known polynomial-time algorithms. What drives this extreme disparity, and do problems exist that lie between these diametrically opposed complexities? In this paper we identify and analyse a sub-class of stochastic shortest path problems (SSPs) for general state-action spaces whose dynamics satisfy a particular drift condition. This construction generalises the traditional, temporal notion of a horizon via decreasing reachability: a property called reductivity. It is shown that optimal policies can be recovered in polynomial-time for reductive SSPs -- via an extension of backwards induction -- with an efficient analogue in reductive MDPs. The practical considerations of the proposed approach are discussed, and numerical verification provided on a canonical optimal liquidation problem.

Reward is not enough: can we liberate AI from the reinforcement learning paradigm?

I present arguments against the hypothesis put forward by Silver, Singh, Precup, and Sutton ( https://www.sciencedirect.com/science/article/pii/S0004370221000862 ) : reward maximization is not enough to explain many activities associated with natural and artificial intelligence including knowledge, learning, perception, social intelligence, evolution, language, generalisation and imitation. I show such reductio ad lucrum has its intellectual origins in the political economy of Homo economicus and substantially overlaps with the radical version of behaviourism. I show why the reinforcement learning paradigm, despite its demonstrable usefulness in some practical application, is an incomplete framework for intelligence -- natural and artificial. Complexities of intelligent behaviour are not simply second-order complications on top of reward maximisation. This fact has profound implications for the development of practically usable, smart, safe and robust artificially intelligent agents.