Adaptive Bayesian Single-Shot Quantum Sensing

Quantum sensing harnesses the unique properties of quantum systems to enable precision measurements of physical quantities such as time, magnetic and electric fields, acceleration, and gravitational gradients well beyond the limits of classical sensors. However, identifying suitable sensing probes and measurement schemes can be a classically intractable task, as it requires optimizing over Hilbert spaces of high dimension. In variational quantum sensing, a probe quantum system is generated via a parameterized quantum circuit (PQC), exposed to an unknown physical parameter through a quantum channel, and measured to collect classical data. PQCs and measurements are typically optimized using offline strategies based on frequentist learning criteria. This paper introduces an adaptive protocol that uses Bayesian inference to optimize the sensing policy via the maximization of the active information gain. The proposed variational methodology is tailored for non-asymptotic regimes where a single probe can be deployed in each time step, and is extended to support the fusion of estimates from multiple quantum sensing agents.

Dynamic Estimation Loss Control in Variational Quantum Sensing via Online Conformal Inference

Quantum sensing exploits non-classical effects to overcome limitations of classical sensors, with applications ranging from gravitational-wave detection to nanoscale imaging. However, practical quantum sensors built on noisy intermediate-scale quantum (NISQ) devices face significant noise and sampling constraints, and current variational quantum sensing (VQS) methods lack rigorous performance guarantees. This paper proposes an online control framework for VQS that dynamically updates the variational parameters while providing deterministic error bars on the estimates. By leveraging online conformal inference techniques, the approach produces sequential estimation sets with a guaranteed long-term risk level. Experiments on a quantum magnetometry task confirm that the proposed dynamic VQS approach maintains the required reliability over time, while still yielding precise estimates. The results demonstrate the practical benefits of combining variational quantum algorithms with online conformal inference to achieve reliable quantum sensing on NISQ devices.

Expected Free Energy-based Planning as Variational Inference

We address the problem of planning under uncertainty, where an agent must choose actions that not only achieve desired outcomes but also reduce uncertainty. Traditional methods often treat exploration and exploitation as separate objectives, lacking a unified inferential foundation. Active inference, grounded in the Free Energy Principle, offers such a foundation by minimizing Expected Free Energy (EFE), a cost function that combines utility with epistemic drives like ambiguity resolution and novelty seeking. However, the computational burden of EFE minimization has remained a major obstacle to its scalability. In this paper, we show that EFE-based planning arises naturally from minimizing a variational free energy functional on a generative model augmented with preference and epistemic priors. This result reinforces theoretical consistency with the Free Energy Principle, by casting planning itself as variational inference. Our formulation yields optimal policies that jointly support goal achievement and information gain, while incorporating a complexity term that accounts for bounded computational resources. This unifying framework connects and extends existing methods, enabling scalable, resource-aware implementations of active inference agents.

Physics-Aware Initialization Refinement in Code-Aided EM for Blind Channel Estimation

This paper addresses the well-known local maximum problem of the expectation-maximization (EM) algorithm in blind intersymbol interference (ISI) channel estimation. This problem primarily results from phase and shift ambiguity during initialization, which blind estimation is inherently unable to distinguish. We propose an effective initialization refinement algorithm that utilizes the decoder output as a model selection metric, incorporating a technique to detect phase and shift ambiguity. Our results show that the proposed algorithm significantly reduces the number of local maximum cases to nearly one-third for a 3-tap ISI channel under highly uncertain initial conditions. The improvement becomes more pronounced as initial errors increase and the channel memory grows. When used in a turbo equalizer, the proposed algorithm is required only in the first turbo iteration, which limits any complexity increase with subsequent iterations.

Categorical Unsupervised Variational Acoustic Clustering

We propose a categorical approach for unsupervised variational acoustic clustering of audio data in the time-frequency domain. The consideration of a categorical distribution enforces sharper clustering even when data points strongly overlap in time and frequency, which is the case for most datasets of urban acoustic scenes. To this end, we use a Gumbel-Softmax distribution as a soft approximation to the categorical distribution, allowing for training via backpropagation. In this settings, the softmax temperature serves as the main mechanism to tune clustering performance. The results show that the proposed model can obtain impressive clustering performance for all considered datasets, even when data points strongly overlap in time and frequency.

Modified Baum-Welch Algorithm for Joint Blind Channel Estimation and Turbo Equalization

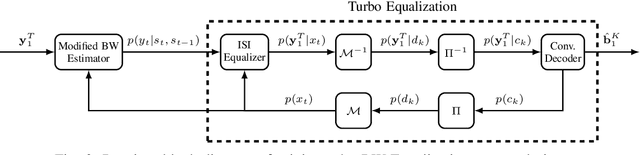
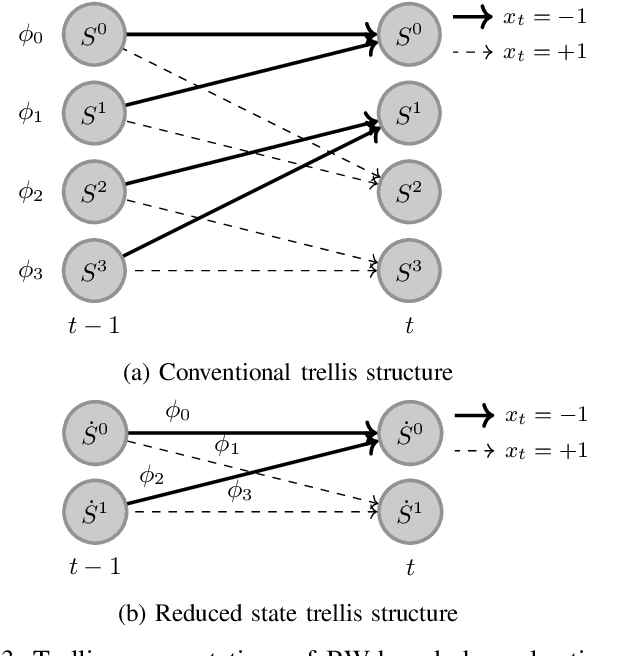
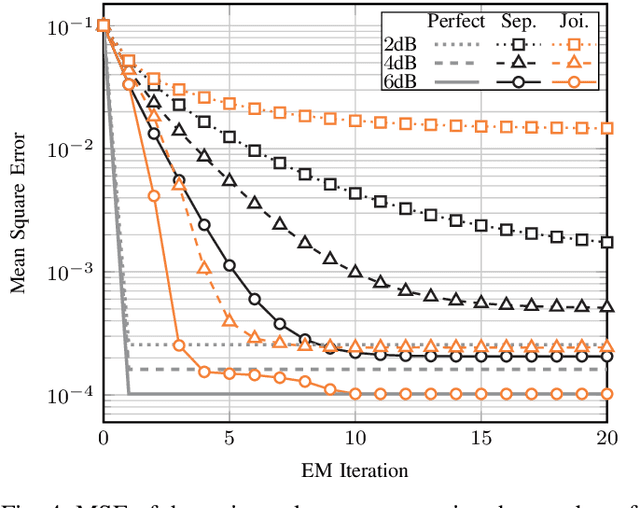
Blind estimation of intersymbol interference channels based on the Baum-Welch (BW) algorithm, a specific implementation of the expectation-maximization (EM) algorithm for training hidden Markov models, is robust and does not require labeled data. However, it is known for its extensive computation cost, slow convergence, and frequently converges to a local maximum. In this paper, we modified the trellis structure of the BW algorithm by associating the channel parameters with two consecutive states. This modification enables us to reduce the number of required states by half while maintaining the same performance. Moreover, to improve the convergence rate and the estimation performance, we construct a joint turbo-BW-equalization system by exploiting the extrinsic information produced by the turbo decoder to refine the BW-based estimator at each EM iteration. Our experiments demonstrate that the joint system achieves convergence in just 4 EM iterations, which is 8 iterations less than a separate system design for a signal-to-noise ratio (SNR) of 6 dB. Additionally, the joint system provides improved estimation accuracy with a mean square error (MSE) of $10^{-4}$. We also identify scenarios where a joint design is not preferable, especially when the channel is noisy (e.g., SNR=2 dB) and the turbo decoder is unable to provide reliable extrinsic information for a BW-based estimator.

Time-Warping Invariant Quantum Recurrent Neural Networks via Quantum-Classical Adaptive Gating

Adaptive gating plays a key role in temporal data processing via classical recurrent neural networks (RNN), as it facilitates retention of past information necessary to predict the future, providing a mechanism that preserves invariance to time warping transformations. This paper builds on quantum recurrent neural networks (QRNNs), a dynamic model with quantum memory, to introduce a novel class of temporal data processing quantum models that preserve invariance to time-warping transformations of the (classical) input-output sequences. The model, referred to as time warping-invariant QRNN (TWI-QRNN), augments a QRNN with a quantum-classical adaptive gating mechanism that chooses whether to apply a parameterized unitary transformation at each time step as a function of the past samples of the input sequence via a classical recurrent model. The TWI-QRNN model class is derived from first principles, and its capacity to successfully implement time-warping transformations is experimentally demonstrated on examples with classical or quantum dynamics.

Learning with Limited Samples -- Meta-Learning and Applications to Communication Systems

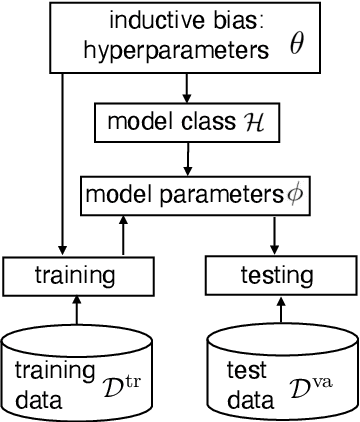
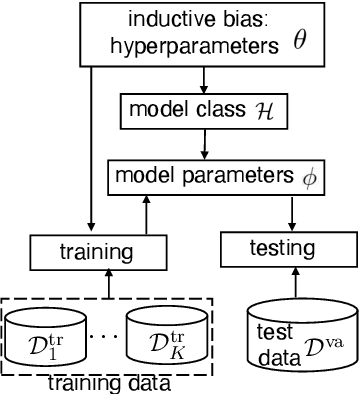
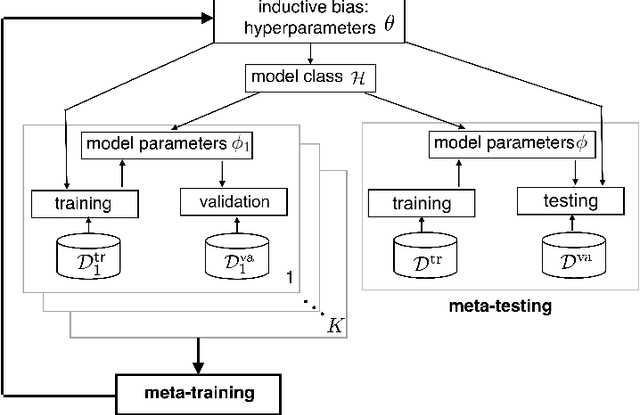
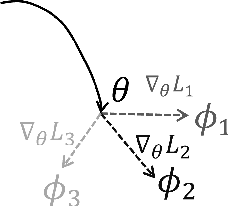
Deep learning has achieved remarkable success in many machine learning tasks such as image classification, speech recognition, and game playing. However, these breakthroughs are often difficult to translate into real-world engineering systems because deep learning models require a massive number of training samples, which are costly to obtain in practice. To address labeled data scarcity, few-shot meta-learning optimizes learning algorithms that can efficiently adapt to new tasks quickly. While meta-learning is gaining significant interest in the machine learning literature, its working principles and theoretic fundamentals are not as well understood in the engineering community. This review monograph provides an introduction to meta-learning by covering principles, algorithms, theory, and engineering applications. After introducing meta-learning in comparison with conventional and joint learning, we describe the main meta-learning algorithms, as well as a general bilevel optimization framework for the definition of meta-learning techniques. Then, we summarize known results on the generalization capabilities of meta-learning from a statistical learning viewpoint. Applications to communication systems, including decoding and power allocation, are discussed next, followed by an introduction to aspects related to the integration of meta-learning with emerging computing technologies, namely neuromorphic and quantum computing. The monograph is concluded with an overview of open research challenges.

Quantum-Aided Meta-Learning for Bayesian Binary Neural Networks via Born Machines

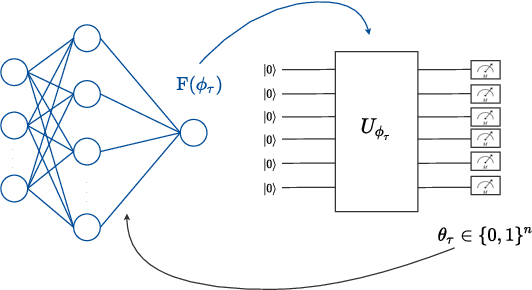
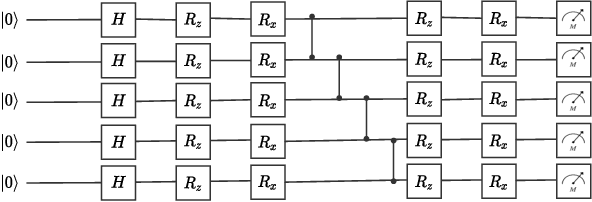
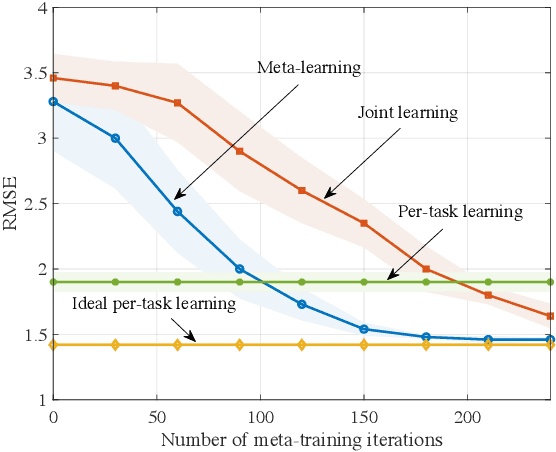
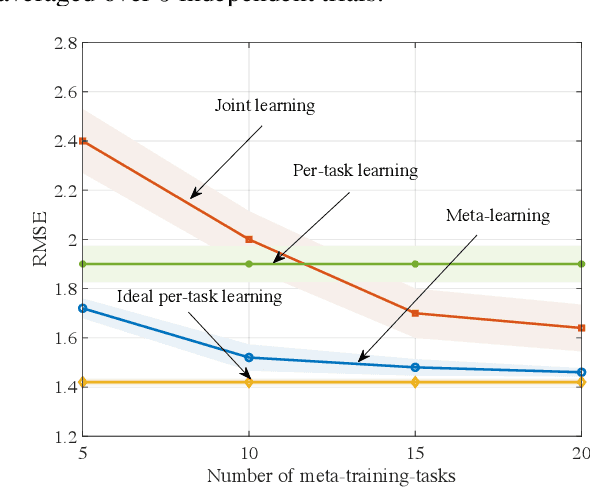
Near-term noisy intermediate-scale quantum circuits can efficiently implement implicit probabilistic models in discrete spaces, supporting distributions that are practically infeasible to sample from using classical means. One of the possible applications of such models, also known as Born machines, is probabilistic inference, which is at the core of Bayesian methods. This paper studies the use of Born machines for the problem of training binary Bayesian neural networks. In the proposed approach, a Born machine is used to model the variational distribution of the binary weights of the neural network, and data from multiple tasks is used to reduce training data requirements on new tasks. The method combines gradient-based meta-learning and variational inference via Born machines, and is shown in a prototypical regression problem to outperform conventional joint learning strategies.

Training Hybrid Classical-Quantum Classifiers via Stochastic Variational Optimization

Quantum machine learning has emerged as a potential practical application of near-term quantum devices. In this work, we study a two-layer hybrid classical-quantum classifier in which a first layer of quantum stochastic neurons implementing generalized linear models (QGLMs) is followed by a second classical combining layer. The input to the first, hidden, layer is obtained via amplitude encoding in order to leverage the exponential size of the fan-in of the quantum neurons in the number of qubits per neuron. To facilitate implementation of the QGLMs, all weights and activations are binary. While the state of the art on training strategies for this class of models is limited to exhaustive search and single-neuron perceptron-like bit-flip strategies, this letter introduces a stochastic variational optimization approach that enables the joint training of quantum and classical layers via stochastic gradient descent. Experiments show the advantages of the approach for a variety of activation functions implemented by QGLM neurons.