Expected Free Energy-based Planning as Variational Inference

We address the problem of planning under uncertainty, where an agent must choose actions that not only achieve desired outcomes but also reduce uncertainty. Traditional methods often treat exploration and exploitation as separate objectives, lacking a unified inferential foundation. Active inference, grounded in the Free Energy Principle, offers such a foundation by minimizing Expected Free Energy (EFE), a cost function that combines utility with epistemic drives like ambiguity resolution and novelty seeking. However, the computational burden of EFE minimization has remained a major obstacle to its scalability. In this paper, we show that EFE-based planning arises naturally from minimizing a variational free energy functional on a generative model augmented with preference and epistemic priors. This result reinforces theoretical consistency with the Free Energy Principle, by casting planning itself as variational inference. Our formulation yields optimal policies that jointly support goal achievement and information gain, while incorporating a complexity term that accounts for bounded computational resources. This unifying framework connects and extends existing methods, enabling scalable, resource-aware implementations of active inference agents.

Realising Synthetic Active Inference Agents, Part I: Epistemic Objectives and Graphical Specification Language

The Free Energy Principle (FEP) is a theoretical framework for describing how (intelligent) systems self-organise into coherent, stable structures by minimising a free energy functional. Active Inference (AIF) is a corollary of the FEP that specifically details how systems that are able to plan for the future (agents) function by minimising particular free energy functionals that incorporate information seeking components. This paper is the first in a series of two where we derive a synthetic version of AIF on free form factor graphs. The present paper focuses on deriving a local version of the free energy functionals used for AIF. This enables us to construct a version of AIF which applies to arbitrary graphical models and interfaces with prior work on message passing algorithms. The resulting messages are derived in our companion paper. We also identify a gap in the graphical notation used for factor graphs. While factor graphs are great at expressing a generative model, they have so far been unable to specify the full optimisation problem including constraints. To solve this problem we develop Constrained Forney-style Factor Graph (CFFG) notation which permits a fully graphical description of variational inference objectives. We then proceed to show how CFFG's can be used to reconstruct prior algorithms for AIF as well as derive new ones. The latter is demonstrated by deriving an algorithm that permits direct policy inference for AIF agents, circumventing a long standing scaling issue that has so far hindered the application of AIF in industrial settings. We demonstrate our algorithm on the classic T-maze task and show that it reproduces the information seeking behaviour that is a hallmark feature of AIF.

Automating Model Comparison in Factor Graphs

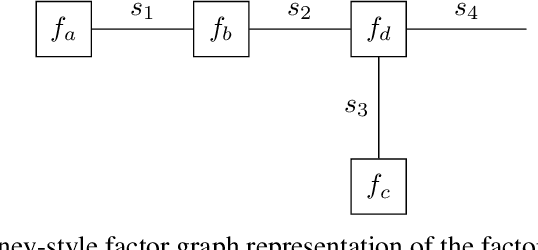
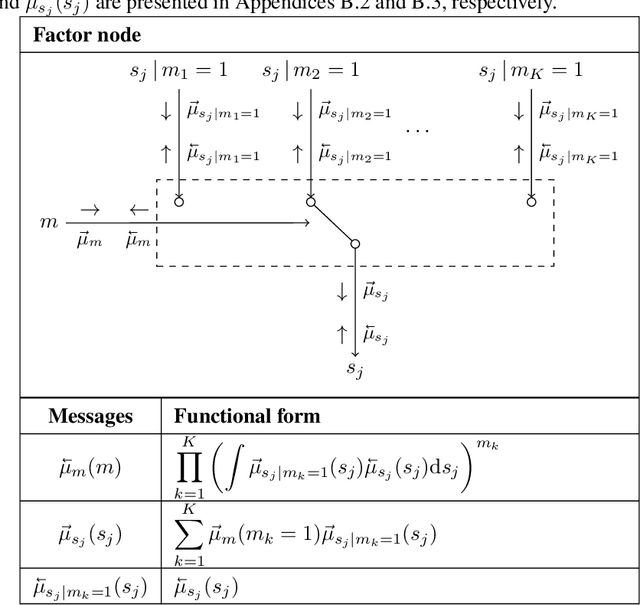
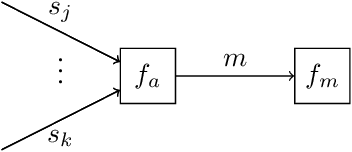
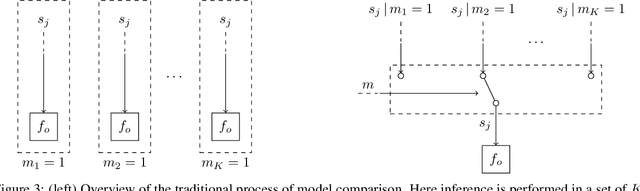
Bayesian state and parameter estimation have been automated effectively in the literature, however, this has not yet been the case for model comparison, which therefore still requires error-prone and time-consuming manual derivations. As a result, model comparison is often overlooked and ignored, despite its importance. This paper efficiently automates Bayesian model averaging, selection, and combination by message passing on a Forney-style factor graph with a custom mixture node. Parameter and state inference, and model comparison can then be executed simultaneously using message passing with scale factors. This approach shortens the model design cycle and allows for the straightforward extension to hierarchical and temporal model priors to accommodate for modeling complicated time-varying processes.

Realising Synthetic Active Inference Agents, Part II: Variational Message Updates

The Free Energy Principle (FEP) describes (biological) agents as minimising a variational Free Energy (FE) with respect to a generative model of their environment. Active Inference (AIF) is a corollary of the FEP that describes how agents explore and exploit their environment by minimising an expected FE objective. In two related papers, we describe a scalable, epistemic approach to synthetic AIF agents, by message passing on free-form Forney-style Factor Graphs (FFGs). A companion paper (part I) introduces a Constrained FFG (CFFG) notation that visually represents (generalised) FE objectives for AIF. The current paper (part II) derives message passing algorithms that minimise (generalised) FE objectives on a CFFG by variational calculus. A comparison between simulated Bethe and generalised FE agents illustrates how synthetic AIF induces epistemic behaviour on a T-maze navigation task. With a full message passing account of synthetic AIF agents, it becomes possible to derive and reuse message updates across models and move closer to industrial applications of synthetic AIF.

Active Inference and Epistemic Value in Graphical Models

The Free Energy Principle (FEP) postulates that biological agents perceive and interact with their environment in order to minimize a Variational Free Energy (VFE) with respect to a generative model of their environment. The inference of a policy (future control sequence) according to the FEP is known as Active Inference (AIF). The AIF literature describes multiple VFE objectives for policy planning that lead to epistemic (information-seeking) behavior. However, most objectives have limited modeling flexibility. This paper approaches epistemic behavior from a constrained Bethe Free Energy (CBFE) perspective. Crucially, variational optimization of the CBFE can be expressed in terms of message passing on free-form generative models. The key intuition behind the CBFE is that we impose a point-mass constraint on predicted outcomes, which explicitly encodes the assumption that the agent will make observations in the future. We interpret the CBFE objective in terms of its constituent behavioral drives. We then illustrate resulting behavior of the CBFE by planning and interacting with a simulated T-maze environment. Simulations for the T-maze task illustrate how the CBFE agent exhibits an epistemic drive, and actively plans ahead to account for the impact of predicted outcomes. Compared to an EFE agent, the CBFE agent incurs expected reward in significantly more environmental scenarios. We conclude that CBFE optimization by message passing suggests a general mechanism for epistemic-aware AIF in free-form generative models.

Chance-Constrained Active Inference

Active Inference (ActInf) is an emerging theory that explains perception and action in biological agents, in terms of minimizing a free energy bound on Bayesian surprise. Goal-directed behavior is elicited by introducing prior beliefs on the underlying generative model. In contrast to prior beliefs, which constrain all realizations of a random variable, we propose an alternative approach through chance constraints, which allow for a (typically small) probability of constraint violation, and demonstrate how such constraints can be used as intrinsic drivers for goal-directed behavior in ActInf. We illustrate how chance-constrained ActInf weights all imposed (prior) constraints on the generative model, allowing e.g., for a trade-off between robust control and empirical chance constraint violation. Secondly, we interpret the proposed solution within a message passing framework. Interestingly, the message passing interpretation is not only relevant to the context of ActInf, but also provides a general purpose approach that can account for chance constraints on graphical models. The chance constraint message updates can then be readily combined with other pre-derived message update rules, without the need for custom derivations. The proposed chance-constrained message passing framework thus accelerates the search for workable models in general, and can be used to complement message-passing formulations on generative neural models.

A Factor Graph Approach to Automated Design of Bayesian Signal Processing Algorithms

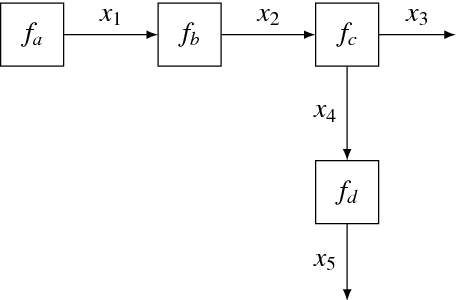
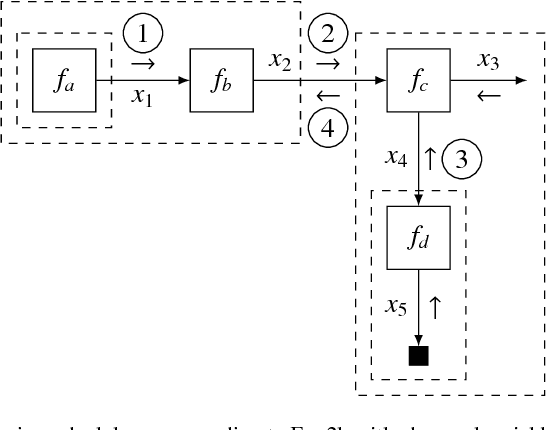
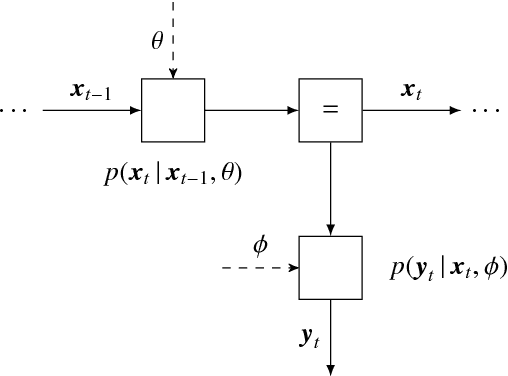
The benefits of automating design cycles for Bayesian inference-based algorithms are becoming increasingly recognized by the machine learning community. As a result, interest in probabilistic programming frameworks has much increased over the past few years. This paper explores a specific probabilistic programming paradigm, namely message passing in Forney-style factor graphs (FFGs), in the context of automated design of efficient Bayesian signal processing algorithms. To this end, we developed "ForneyLab" (https://github.com/biaslab/ForneyLab.jl) as a Julia toolbox for message passing-based inference in FFGs. We show by example how ForneyLab enables automatic derivation of Bayesian signal processing algorithms, including algorithms for parameter estimation and model comparison. Crucially, due to the modular makeup of the FFG framework, both the model specification and inference methods are readily extensible in ForneyLab. In order to test this framework, we compared variational message passing as implemented by ForneyLab with automatic differentiation variational inference (ADVI) and Monte Carlo methods as implemented by state-of-the-art tools "Edward" and "Stan". In terms of performance, extensibility and stability issues, ForneyLab appears to enjoy an edge relative to its competitors for automated inference in state-space models.

A Probabilistic Modeling Approach to Hearing Loss Compensation

Hearing Aid (HA) algorithms need to be tuned ("fitted") to match the impairment of each specific patient. The lack of a fundamental HA fitting theory is a strong contributing factor to an unsatisfying sound experience for about 20% of hearing aid patients. This paper proposes a probabilistic modeling approach to the design of HA algorithms. The proposed method relies on a generative probabilistic model for the hearing loss problem and provides for automated inference of the corresponding (1) signal processing algorithm, (2) the fitting solution as well as a principled (3) performance evaluation metric. All three tasks are realized as message passing algorithms in a factor graph representation of the generative model, which in principle allows for fast implementation on hearing aid or mobile device hardware. The methods are theoretically worked out and simulated with a custom-built factor graph toolbox for a specific hearing loss model.