Zero-Shot Temporal Resolution Domain Adaptation for Spiking Neural Networks

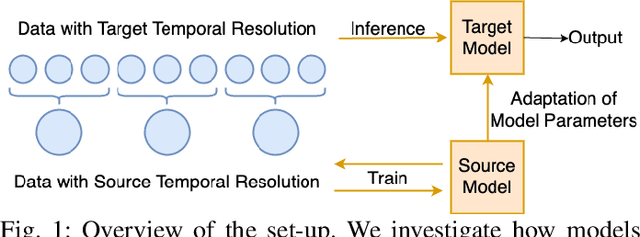
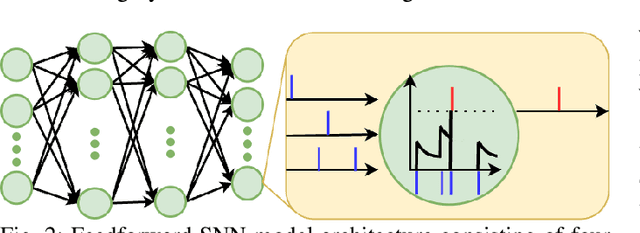
Spiking Neural Networks (SNNs) are biologically-inspired deep neural networks that efficiently extract temporal information while offering promising gains in terms of energy efficiency and latency when deployed on neuromorphic devices. However, SNN model parameters are sensitive to temporal resolution, leading to significant performance drops when the temporal resolution of target data at the edge is not the same with that of the pre-deployment source data used for training, especially when fine-tuning is not possible at the edge. To address this challenge, we propose three novel domain adaptation methods for adapting neuron parameters to account for the change in time resolution without re-training on target time-resolution. The proposed methods are based on a mapping between neuron dynamics in SNNs and State Space Models (SSMs); and are applicable to general neuron models. We evaluate the proposed methods under spatio-temporal data tasks, namely the audio keyword spotting datasets SHD and MSWC as well as the image classification NMINST dataset. Our methods provide an alternative to - and in majority of the cases significantly outperform - the existing reference method that simply scales the time constant. Moreover, our results show that high accuracy on high temporal resolution data can be obtained by time efficient training on lower temporal resolution data and model adaptation.

Distributed Continual Learning with CoCoA in High-dimensional Linear Regression

We consider estimation under scenarios where the signals of interest exhibit change of characteristics over time. In particular, we consider the continual learning problem where different tasks, e.g., data with different distributions, arrive sequentially and the aim is to perform well on the newly arrived task without performance degradation on the previously seen tasks. In contrast to the continual learning literature focusing on the centralized setting, we investigate the problem from a distributed estimation perspective. We consider the well-established distributed learning algorithm COCOA, which distributes the model parameters and the corresponding features over the network. We provide exact analytical characterization for the generalization error of COCOA under continual learning for linear regression in a range of scenarios, where overparameterization is of particular interest. These analytical results characterize how the generalization error depends on the network structure, the task similarity and the number of tasks, and show how these dependencies are intertwined. In particular, our results show that the generalization error can be significantly reduced by adjusting the network size, where the most favorable network size depends on task similarity and the number of tasks. We present numerical results verifying the theoretical analysis and illustrate the continual learning performance of COCOA with a digit classification task.

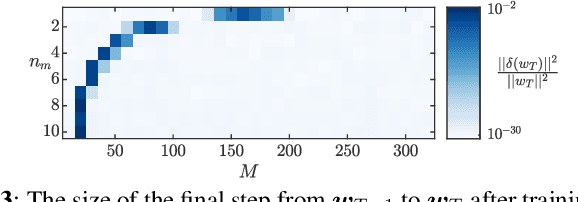
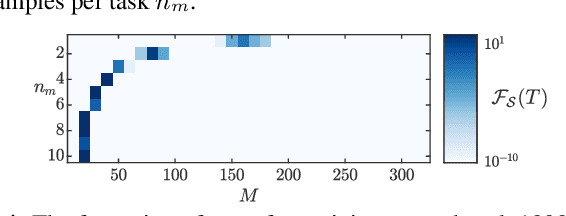
Continual Learning with Distributed Optimization: Does CoCoA Forget?

We focus on the continual learning problem where the tasks arrive sequentially and the aim is to perform well on the newly arrived task without performance degradation on the previously seen tasks. In contrast to the continual learning literature focusing on the centralized setting, we investigate the distributed estimation framework. We consider the well-established distributed learning algorithm CoCoA. We derive closed form expressions for the iterations for the overparametrized case. We illustrate the convergence and the error performance of the algorithm based on the over/under-parametrization of the problem. Our results show that depending on the problem dimensions and data generation assumptions, CoCoA can perform continual learning over a sequence of tasks, i.e., it can learn a new task without forgetting previously learned tasks, with access only to one task at a time.

Regularization with Fake Features

Recent successes of massively overparameterized models have inspired a new line of work investigating the underlying conditions that enable overparameterized models to generalize well. This paper considers a framework where the possibly overparametrized model includes fake features, i.e., features that are present in the model but not in the data. We present a non-asymptotic high-probability bound on the generalization error of the ridge regression problem under the model misspecification of having fake features. Our high-probability results characterize the interplay between the implicit regularization provided by the fake features and the explicit regularization provided by the ridge parameter. We observe that fake features may improve the generalization error, even though they are irrelevant to the data.

Estimation and Model Misspecification: Fake and Missing Features

We consider estimation under model misspecification where there is a model mismatch between the underlying system, which generates the data, and the model used during estimation. We propose a model misspecification framework which enables a joint treatment of the model misspecification types of having fake and missing features, as well as incorrect covariance assumptions on the unknowns and the noise. Here, features which are included in the model but are not present in the underlying system, and features which are not included in the model but are present in the underlying system, are referred to as fake and missing features, respectively. Under this framework, we characterize the estimation performance and reveal trade-offs between the missing and fake features and the possibly incorrect noise level assumption. In contrast to existing work focusing on incorrect covariance assumptions or missing features, fake features is a central component of our framework. Our results show that fake features can significantly improve the estimation performance, even though they are not correlated with the features in the underlying system. In particular, we show that the estimation error can be decreased by including more fake features in the model, even to the point where the model is overparametrized, i.e., the model contains more unknowns than observations.

Model Mismatch Trade-offs in LMMSE Estimation

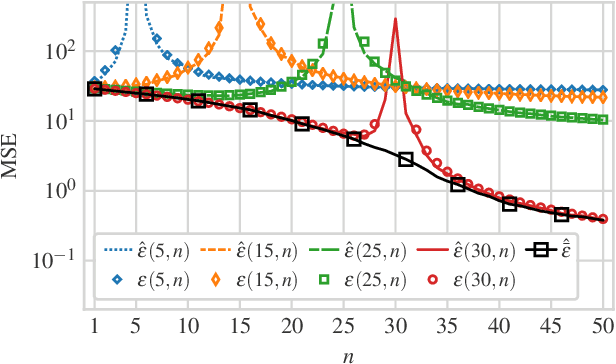
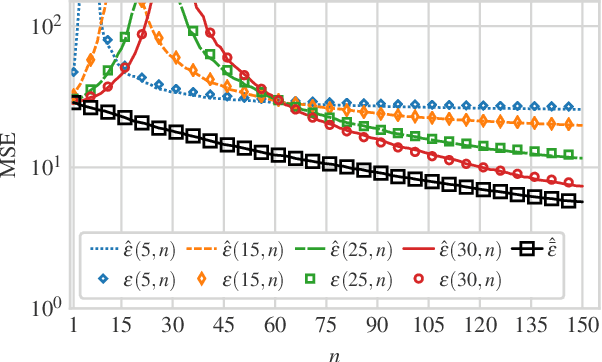
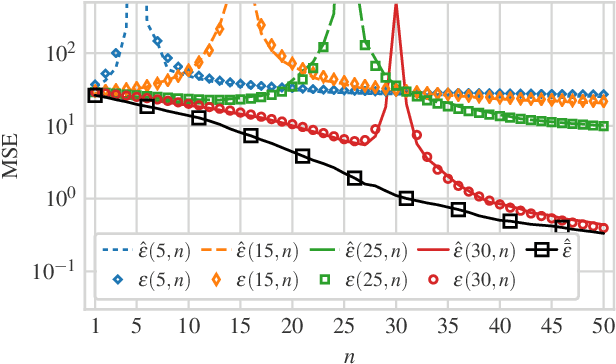
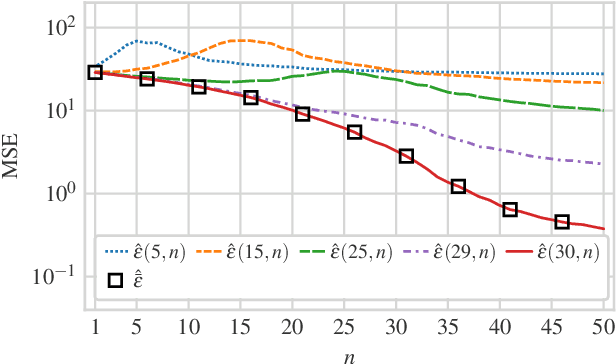
We consider a linear minimum mean squared error (LMMSE) estimation framework with model mismatch where the assumed model order is smaller than that of the underlying linear system which generates the data used in the estimation process. By modelling the regressors of the underlying system as random variables, we analyze the average behaviour of the mean squared error (MSE). Our results quantify how the MSE depends on the interplay between the number of samples and the number of parameters in the underlying system and in the assumed model. In particular, if the number of samples is not sufficiently large, neither increasing the number of samples nor the assumed model complexity is sufficient to guarantee a performance improvement.

Chance-Constrained Active Inference

Active Inference (ActInf) is an emerging theory that explains perception and action in biological agents, in terms of minimizing a free energy bound on Bayesian surprise. Goal-directed behavior is elicited by introducing prior beliefs on the underlying generative model. In contrast to prior beliefs, which constrain all realizations of a random variable, we propose an alternative approach through chance constraints, which allow for a (typically small) probability of constraint violation, and demonstrate how such constraints can be used as intrinsic drivers for goal-directed behavior in ActInf. We illustrate how chance-constrained ActInf weights all imposed (prior) constraints on the generative model, allowing e.g., for a trade-off between robust control and empirical chance constraint violation. Secondly, we interpret the proposed solution within a message passing framework. Interestingly, the message passing interpretation is not only relevant to the context of ActInf, but also provides a general purpose approach that can account for chance constraints on graphical models. The chance constraint message updates can then be readily combined with other pre-derived message update rules, without the need for custom derivations. The proposed chance-constrained message passing framework thus accelerates the search for workable models in general, and can be used to complement message-passing formulations on generative neural models.

Linear Regression with Distributed Learning: A Generalization Error Perspective

Distributed learning provides an attractive framework for scaling the learning task by sharing the computational load over multiple nodes in a network. Here, we investigate the performance of distributed learning for large-scale linear regression where the model parameters, i.e., the unknowns, are distributed over the network. We adopt a statistical learning approach. In contrast to works that focus on the performance on the training data, we focus on the generalization error, i.e., the performance on unseen data. We provide high-probability bounds on the generalization error for both isotropic and correlated Gaussian data as well as sub-gaussian data. These results reveal the dependence of the generalization performance on the partitioning of the model over the network. In particular, our results show that the generalization error of the distributed solution can be substantially higher than that of the centralized solution even when the error on the training data is at the same level for both the centralized and distributed approaches. Our numerical results illustrate the performance with both real-world image data as well as synthetic data.

Generalization Error for Linear Regression under Distributed Learning

Distributed learning facilitates the scaling-up of data processing by distributing the computational burden over several nodes. Despite the vast interest in distributed learning, generalization performance of such approaches is not well understood. We address this gap by focusing on a linear regression setting. We consider the setting where the unknowns are distributed over a network of nodes. We present an analytical characterization of the dependence of the generalization error on the partitioning of the unknowns over nodes. In particular, for the overparameterized case, our results show that while the error on training data remains in the same range as that of the centralized solution, the generalization error of the distributed solution increases dramatically compared to that of the centralized solution when the number of unknowns estimated at any node is close to the number of observations. We further provide numerical examples to verify our analytical expressions.