Model Mismatch Trade-offs in LMMSE Estimation
Paper and Code
May 25, 2021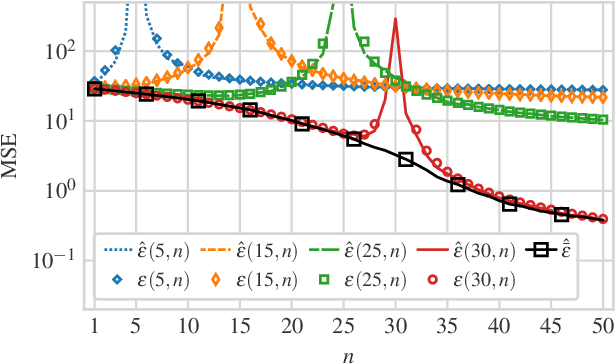
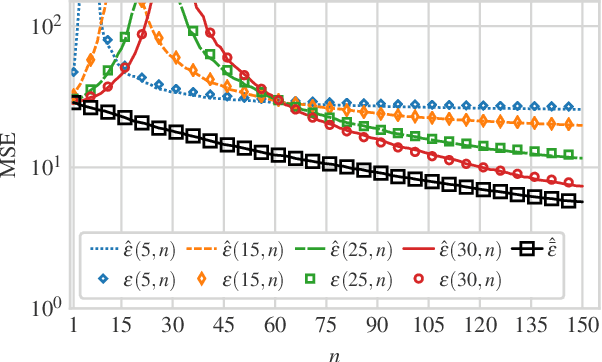
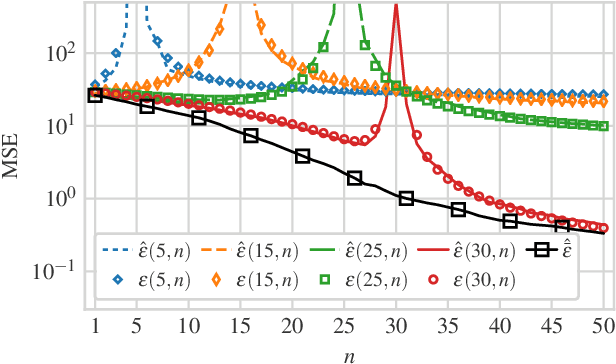
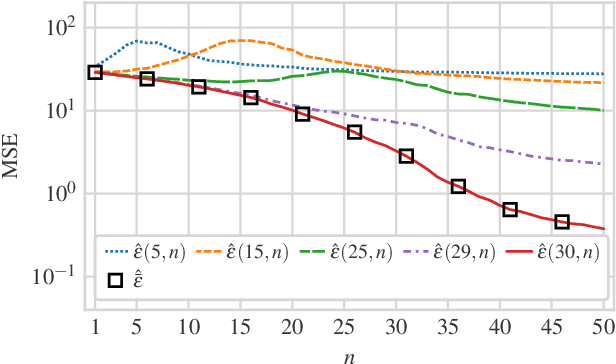
We consider a linear minimum mean squared error (LMMSE) estimation framework with model mismatch where the assumed model order is smaller than that of the underlying linear system which generates the data used in the estimation process. By modelling the regressors of the underlying system as random variables, we analyze the average behaviour of the mean squared error (MSE). Our results quantify how the MSE depends on the interplay between the number of samples and the number of parameters in the underlying system and in the assumed model. In particular, if the number of samples is not sufficiently large, neither increasing the number of samples nor the assumed model complexity is sufficient to guarantee a performance improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge