Low-Bit Data Processing Using Multiple-Output Spiking Neurons with Non-linear Reset Feedback

Neuromorphic computing is an emerging technology enabling low-latency and energy-efficient signal processing. A key algorithmic tool in neuromorphic computing is spiking neural networks (SNNs). SNNs are biologically inspired neural networks which utilize stateful neurons, and provide low-bit data processing by encoding and decoding information using spikes. Similar to SNNs, deep state-space models (SSMs) utilize stateful building blocks. However, deep SSMs, which recently achieved competitive performance in various temporal modeling tasks, are typically designed with high-precision activation functions and no reset mechanisms. To bridge the gains offered by SNNs and the recent deep SSM models, we propose a novel multiple-output spiking neuron model that combines a linear, general SSM state transition with a non-linear feedback mechanism through reset. Compared to the existing neuron models for SNNs, our proposed model clearly conceptualizes the differences between the spiking function, the reset condition and the reset action. The experimental results on various tasks, i.e., a keyword spotting task, an event-based vision task and a sequential pattern recognition task, show that our proposed model achieves performance comparable to existing benchmarks in the SNN literature. Our results illustrate how the proposed reset mechanism can overcome instability and enable learning even when the linear part of neuron dynamics is unstable, allowing us to go beyond the strictly enforced stability of linear dynamics in recent deep SSM models.

State-Space Model Inspired Multiple-Input Multiple-Output Spiking Neurons

In spiking neural networks (SNNs), the main unit of information processing is the neuron with an internal state. The internal state generates an output spike based on its component associated with the membrane potential. This spike is then communicated to other neurons in the network. Here, we propose a general multiple-input multiple-output (MIMO) spiking neuron model that goes beyond this traditional single-input single-output (SISO) model in the SNN literature. Our proposed framework is based on interpreting the neurons as state-space models (SSMs) with linear state evolutions and non-linear spiking activation functions. We illustrate the trade-offs among various parameters of the proposed SSM-inspired neuron model, such as the number of hidden neuron states, the number of input and output channels, including single-input multiple-output (SIMO) and multiple-input single-output (MISO) models. We show that for SNNs with a small number of neurons with large internal state spaces, significant performance gains may be obtained by increasing the number of output channels of a neuron. In particular, a network with spiking neurons with multiple-output channels may achieve the same level of accuracy with the baseline with the continuous-valued communications on the same reference network architecture.

Distributed Average Consensus via Noisy and Non-Coherent Over-the-Air Aggregation

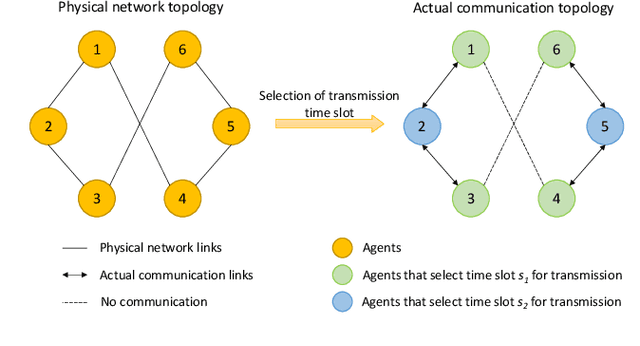
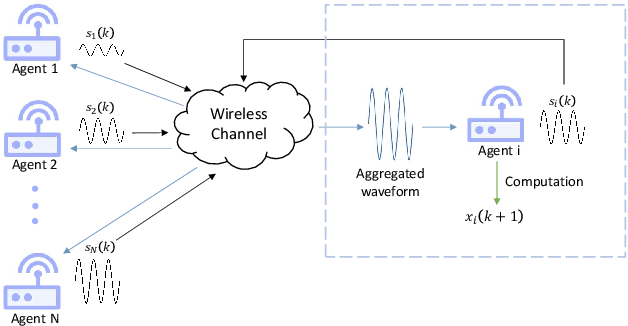
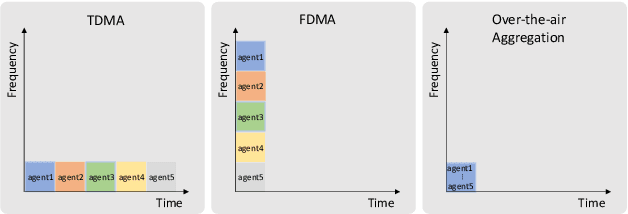
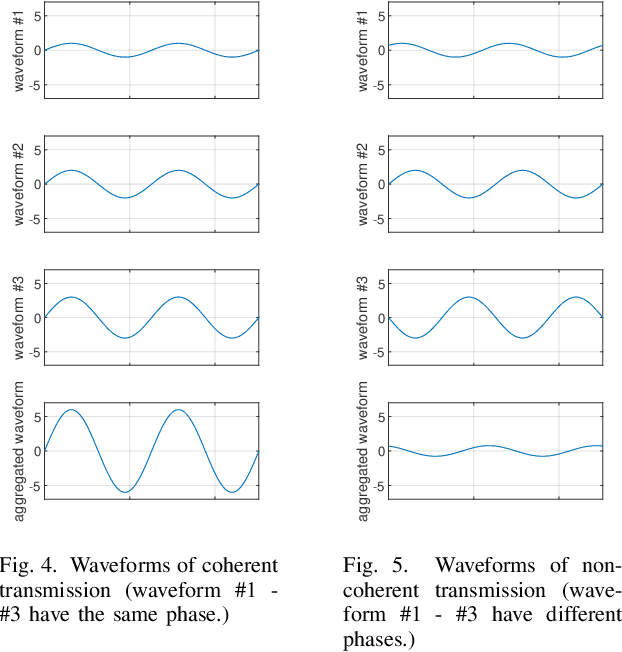
Over-the-air aggregation has attracted widespread attention for its potential advantages in task-oriented applications, such as distributed sensing, learning, and consensus. In this paper, we develop a communication-efficient distributed average consensus protocol by utilizing over-the-air aggregation, which exploits the superposition property of wireless channels rather than combat it. Noisy channels and non-coherent transmission are taken into account, and only half-duplex transceivers are required. We prove that the system can achieve average consensus in mean square and even almost surely under the proposed protocol. Furthermore, we extend the analysis to the scenarios with time-varying topology. Numerical simulation shows the effectiveness of the proposed protocol.

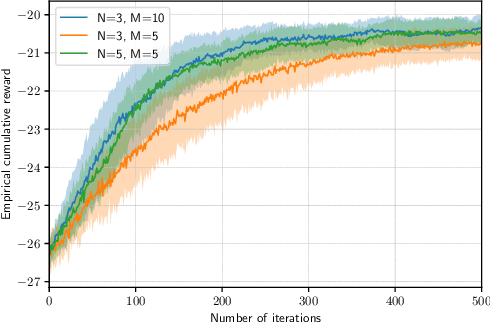
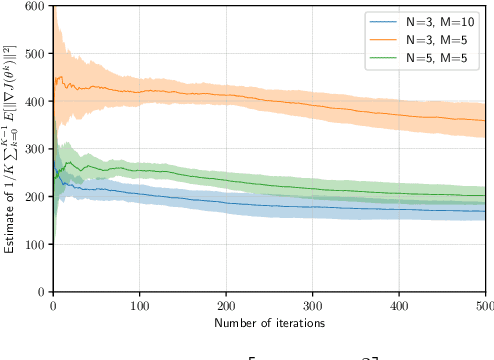
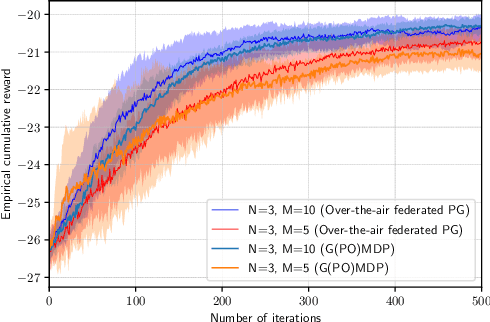
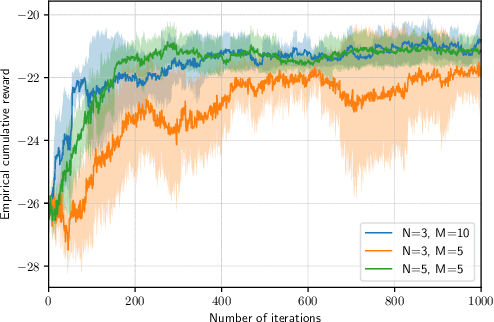
Over-the-air Federated Policy Gradient

In recent years, over-the-air aggregation has been widely considered in large-scale distributed learning, optimization, and sensing. In this paper, we propose the over-the-air federated policy gradient algorithm, where all agents simultaneously broadcast an analog signal carrying local information to a common wireless channel, and a central controller uses the received aggregated waveform to update the policy parameters. We investigate the effect of noise and channel distortion on the convergence of the proposed algorithm, and establish the complexities of communication and sampling for finding an $\epsilon$-approximate stationary point. Finally, we present some simulation results to show the effectiveness of the algorithm.

FedZeN: Towards superlinear zeroth-order federated learning via incremental Hessian estimation

Federated learning is a distributed learning framework that allows a set of clients to collaboratively train a model under the orchestration of a central server, without sharing raw data samples. Although in many practical scenarios the derivatives of the objective function are not available, only few works have considered the federated zeroth-order setting, in which functions can only be accessed through a budgeted number of point evaluations. In this work we focus on convex optimization and design the first federated zeroth-order algorithm to estimate the curvature of the global objective, with the purpose of achieving superlinear convergence. We take an incremental Hessian estimator whose error norm converges linearly, and we adapt it to the federated zeroth-order setting, sampling the random search directions from the Stiefel manifold for improved performance. In particular, both the gradient and Hessian estimators are built at the central server in a communication-efficient and privacy-preserving way by leveraging synchronized pseudo-random number generators. We provide a theoretical analysis of our algorithm, named FedZeN, proving local quadratic convergence with high probability and global linear convergence up to zeroth-order precision. Numerical simulations confirm the superlinear convergence rate and show that our algorithm outperforms the federated zeroth-order methods available in the literature.

Q-SHED: Distributed Optimization at the Edge via Hessian Eigenvectors Quantization

Edge networks call for communication efficient (low overhead) and robust distributed optimization (DO) algorithms. These are, in fact, desirable qualities for DO frameworks, such as federated edge learning techniques, in the presence of data and system heterogeneity, and in scenarios where internode communication is the main bottleneck. Although computationally demanding, Newton-type (NT) methods have been recently advocated as enablers of robust convergence rates in challenging DO problems where edge devices have sufficient computational power. Along these lines, in this work we propose Q-SHED, an original NT algorithm for DO featuring a novel bit-allocation scheme based on incremental Hessian eigenvectors quantization. The proposed technique is integrated with the recent SHED algorithm, from which it inherits appealing features like the small number of required Hessian computations, while being bandwidth-versatile at a bit-resolution level. Our empirical evaluation against competing approaches shows that Q-SHED can reduce by up to 60% the number of communication rounds required for convergence.

Network-GIANT: Fully distributed Newton-type optimization via harmonic Hessian consensus

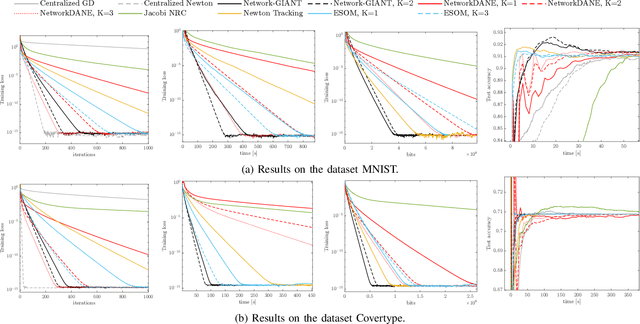
This paper considers the problem of distributed multi-agent learning, where the global aim is to minimize a sum of local objective (empirical loss) functions through local optimization and information exchange between neighbouring nodes. We introduce a Newton-type fully distributed optimization algorithm, Network-GIANT, which is based on GIANT, a Federated learning algorithm that relies on a centralized parameter server. The Network-GIANT algorithm is designed via a combination of gradient-tracking and a Newton-type iterative algorithm at each node with consensus based averaging of local gradient and Newton updates. We prove that our algorithm guarantees semi-global and exponential convergence to the exact solution over the network assuming strongly convex and smooth loss functions. We provide empirical evidence of the superior convergence performance of Network-GIANT over other state-of-art distributed learning algorithms such as Network-DANE and Newton-Raphson Consensus.

A Newton-type algorithm for federated learning based on incremental Hessian eigenvector sharing

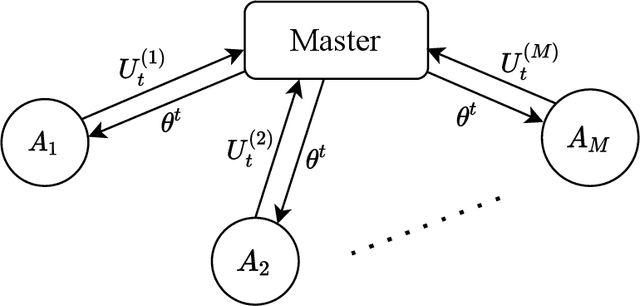
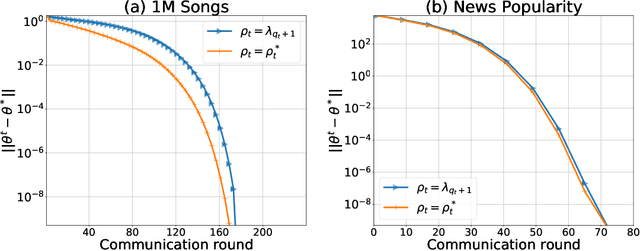
There is a growing interest in the decentralized optimization framework that goes under the name of Federated Learning (FL). In particular, much attention is being turned to FL scenarios where the network is strongly heterogeneous in terms of communication resources (e.g., bandwidth) and data distribution. In these cases, communication between local machines (agents) and the central server (Master) is a main consideration. In this work, we present an original communication-constrained Newton-type (NT) algorithm designed to accelerate FL in such heterogeneous scenarios. The algorithm is by design robust to non i.i.d. data distributions, handles heterogeneity of agents' communication resources (CRs), only requires sporadic Hessian computations, and achieves super-linear convergence. This is possible thanks to an incremental strategy, based on a singular value decomposition (SVD) of the local Hessian matrices, which exploits (possibly) outdated second-order information. The proposed solution is thoroughly validated on real datasets by assessing (i) the number of communication rounds required for convergence, (ii) the overall amount of data transmitted and (iii) the number of local Hessian computations required. For all these metrics, the proposed approach shows superior performance against state-of-the art techniques like GIANT and FedNL.