Network-GIANT: Fully distributed Newton-type optimization via harmonic Hessian consensus
Paper and Code
May 13, 2023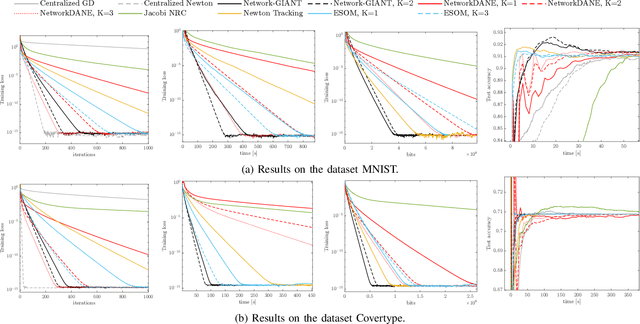
This paper considers the problem of distributed multi-agent learning, where the global aim is to minimize a sum of local objective (empirical loss) functions through local optimization and information exchange between neighbouring nodes. We introduce a Newton-type fully distributed optimization algorithm, Network-GIANT, which is based on GIANT, a Federated learning algorithm that relies on a centralized parameter server. The Network-GIANT algorithm is designed via a combination of gradient-tracking and a Newton-type iterative algorithm at each node with consensus based averaging of local gradient and Newton updates. We prove that our algorithm guarantees semi-global and exponential convergence to the exact solution over the network assuming strongly convex and smooth loss functions. We provide empirical evidence of the superior convergence performance of Network-GIANT over other state-of-art distributed learning algorithms such as Network-DANE and Newton-Raphson Consensus.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge