What Type of Inference is Active Inference?

Active inference casts decision-making as inference, with the Expected Free Energy (EFE) unifying goal-directed and information-seeking behavior. Recent work showed that EFE minimization can be written as Variational Free Energy (VFE) minimization on a generative model augmented with epistemic priors. We prove that the VFE of the augmented model can be rewritten as the VFE of the predictive model plus explicit entropy-correction terms, making the EFE contribution transparent. We then show that proper EFE-based planning requires combining these epistemic corrections with a planning correction that turns marginal inference into policy optimization, yielding a full variational characterization of EFE-based planning. This clarifies which corrections are needed for cross-entropy planning and for full EFE-based planning. The same entropy-corrected formulation leads to a detailed message-passing scheme for EFE-based planning together with simpler ablations. Experiments on three grid-world environments show that the planning correction already helps when observations are decisive, whereas the additional observation-side epistemic corrections matter most when observations are merely suggestive.

Node classification in random trees

We propose a method for the classification of objects that are structured as random trees. Our aim is to model a distribution over the node label assignments in settings where the tree data structure is associated with node attributes (typically high dimensional embeddings). The tree topology is not predetermined and none of the label assignments are present during inference. Other methods that produce a distribution over node label assignment in trees (or more generally in graphs) either assume conditional independence of the label assignment, operate on a fixed graph topology, or require part of the node labels to be observed. Our method defines a Markov Network with the corresponding topology of the random tree and an associated Gibbs distribution. We parameterize the Gibbs distribution with a Graph Neural Network that operates on the random tree and the node embeddings. This allows us to estimate the likelihood of node assignments for a given random tree and use MCMC to sample from the distribution of node assignments. We evaluate our method on the tasks of node classification in trees on the Stanford Sentiment Treebank dataset. Our method outperforms the baselines on this dataset, demonstrating its effectiveness for modeling joint distributions of node labels in random trees.

Automating Model Comparison in Factor Graphs

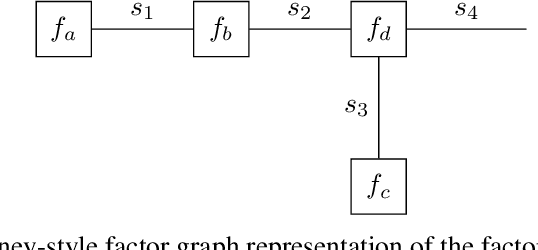
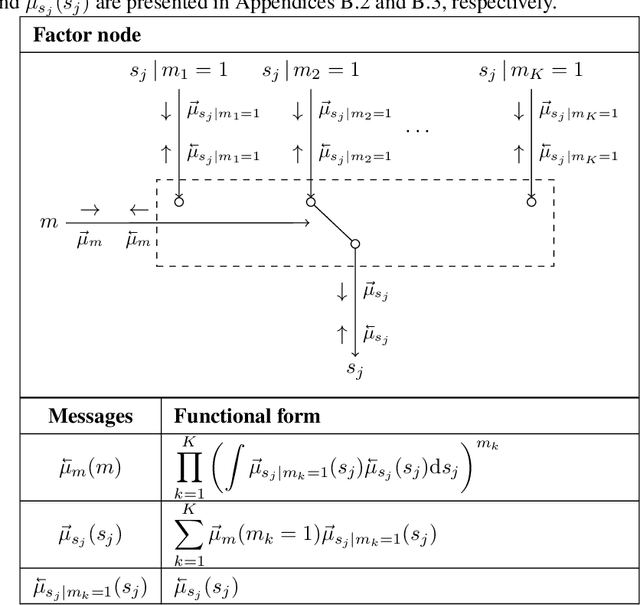
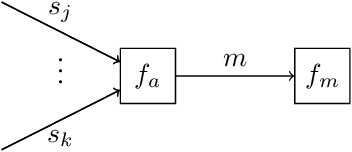
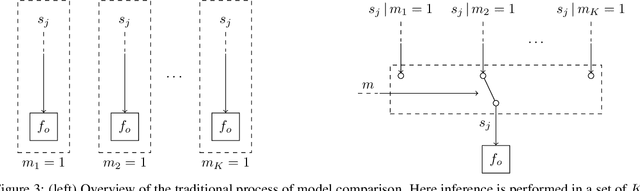
Bayesian state and parameter estimation have been automated effectively in the literature, however, this has not yet been the case for model comparison, which therefore still requires error-prone and time-consuming manual derivations. As a result, model comparison is often overlooked and ignored, despite its importance. This paper efficiently automates Bayesian model averaging, selection, and combination by message passing on a Forney-style factor graph with a custom mixture node. Parameter and state inference, and model comparison can then be executed simultaneously using message passing with scale factors. This approach shortens the model design cycle and allows for the straightforward extension to hierarchical and temporal model priors to accommodate for modeling complicated time-varying processes.