On Sequential Bayesian Optimization with Pairwise Comparison

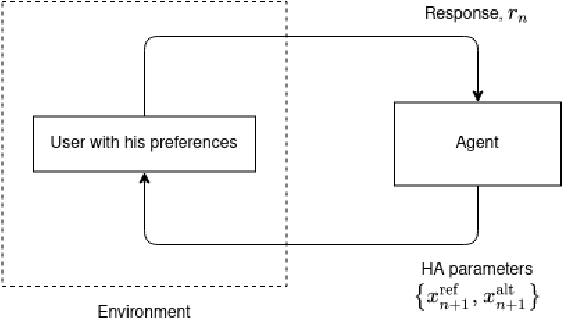
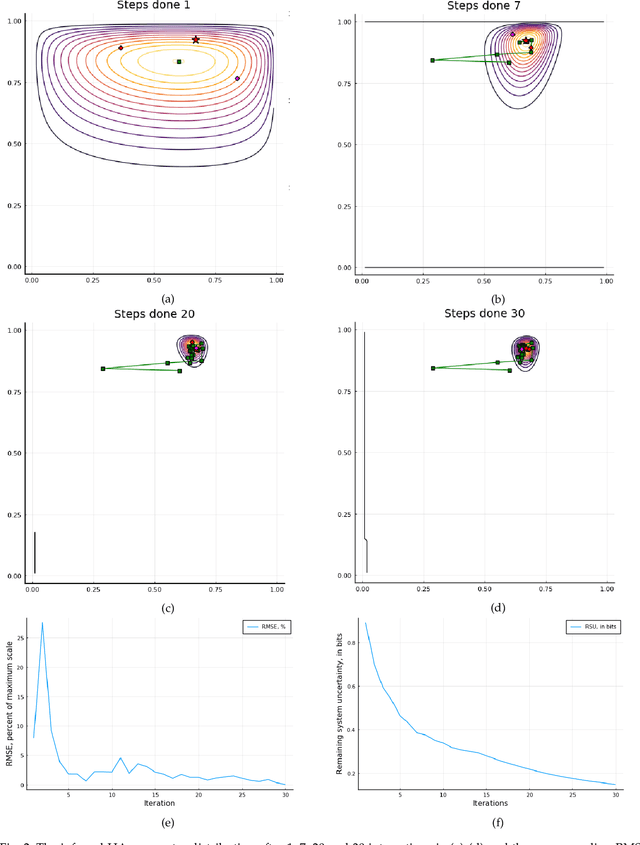
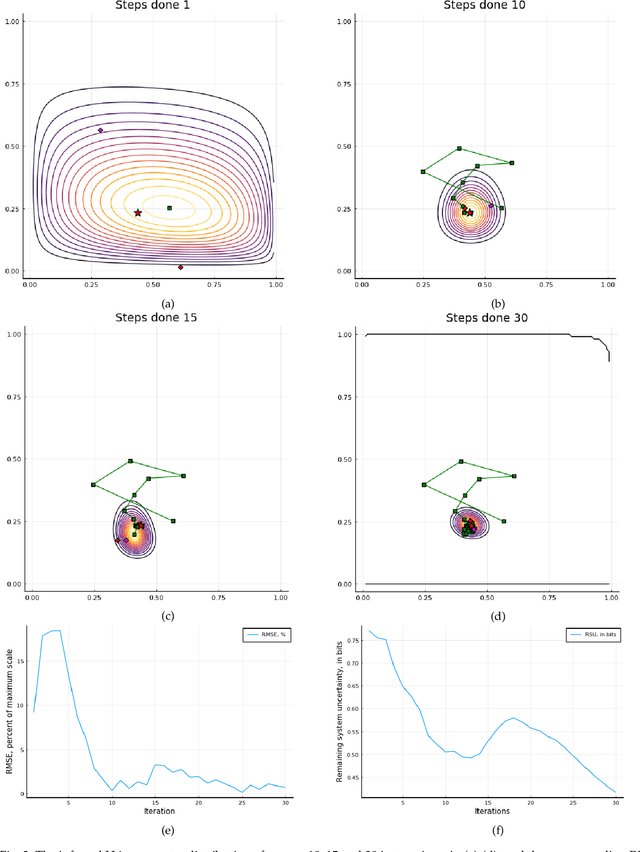
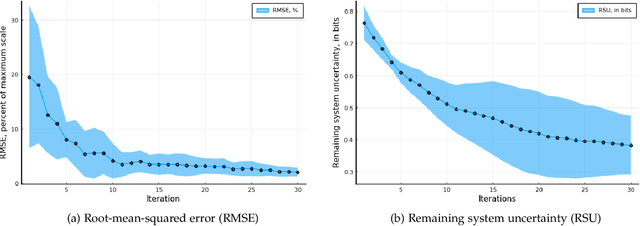
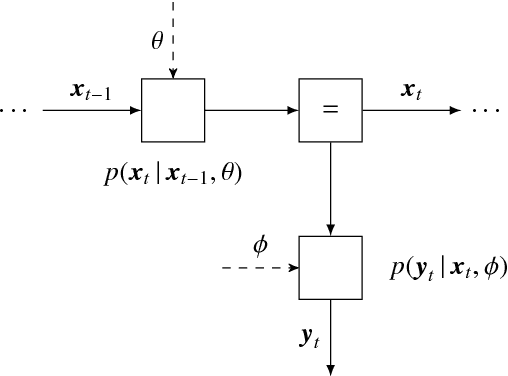
In this work, we study the problem of user preference learning on the example of parameter setting for a hearing aid (HA). We propose to use an agent that interacts with a HA user, in order to collect the most informative data, and learns user preferences for HA parameter settings, based on these data. We model the HA system as two interacting sub-systems, one representing a user with his/her preferences and another one representing an agent. In this system, the user responses to HA settings, proposed by the agent. In our user model, the responses are driven by a parametric user preference function. The agent comprises the sequential mechanisms for user model inference and HA parameter proposal generation. To infer the user model (preference function), Bayesian approximate inference is used in the agent. Here we propose the normalized weighted Kullback-Leibler (KL) divergence between true and agent-assigned predictive user response distributions as a metric to assess the quality of learned preferences. Moreover, our agent strategy for generating HA parameter proposals is to generate HA settings, responses to which help resolving uncertainty associated with prediction of the user responses the most. The resulting data, consequently, allows for efficient user model learning. The normalized weighted KL-divergence plays an important role here as well, since it characterizes the informativeness of the data to be used for probing the user. The efficiency of our approach is validated by numerical simulations.

A Factor Graph Approach to Automated Design of Bayesian Signal Processing Algorithms

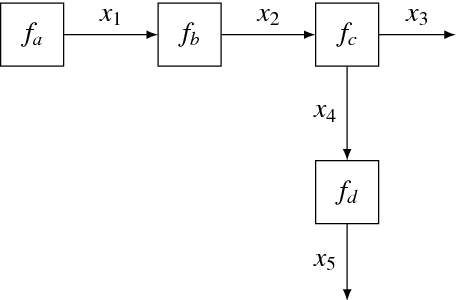
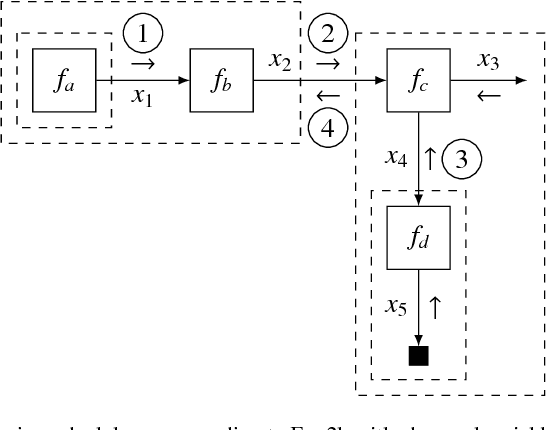
The benefits of automating design cycles for Bayesian inference-based algorithms are becoming increasingly recognized by the machine learning community. As a result, interest in probabilistic programming frameworks has much increased over the past few years. This paper explores a specific probabilistic programming paradigm, namely message passing in Forney-style factor graphs (FFGs), in the context of automated design of efficient Bayesian signal processing algorithms. To this end, we developed "ForneyLab" (https://github.com/biaslab/ForneyLab.jl) as a Julia toolbox for message passing-based inference in FFGs. We show by example how ForneyLab enables automatic derivation of Bayesian signal processing algorithms, including algorithms for parameter estimation and model comparison. Crucially, due to the modular makeup of the FFG framework, both the model specification and inference methods are readily extensible in ForneyLab. In order to test this framework, we compared variational message passing as implemented by ForneyLab with automatic differentiation variational inference (ADVI) and Monte Carlo methods as implemented by state-of-the-art tools "Edward" and "Stan". In terms of performance, extensibility and stability issues, ForneyLab appears to enjoy an edge relative to its competitors for automated inference in state-space models.