Quantum-Aided Meta-Learning for Bayesian Binary Neural Networks via Born Machines
Paper and Code
Apr 05, 2022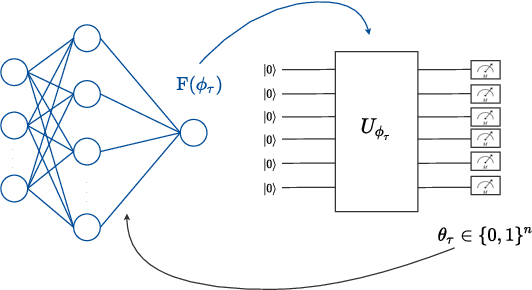
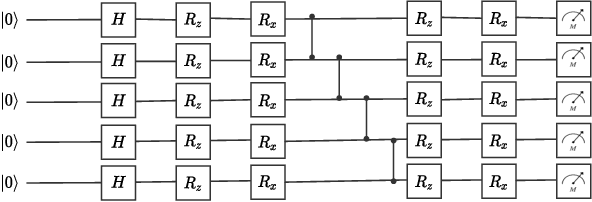
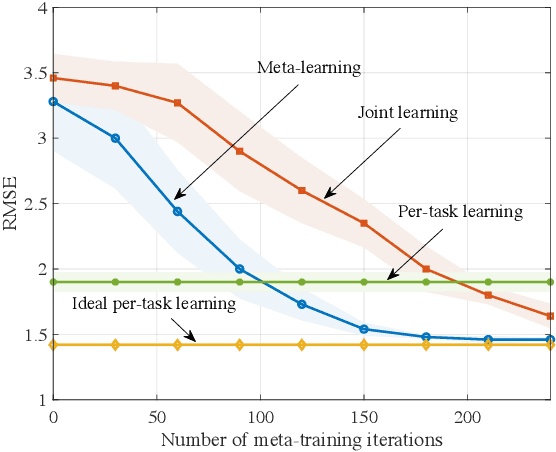
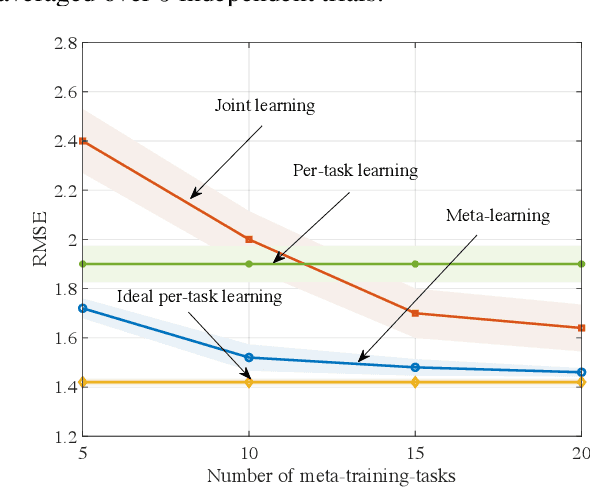
Near-term noisy intermediate-scale quantum circuits can efficiently implement implicit probabilistic models in discrete spaces, supporting distributions that are practically infeasible to sample from using classical means. One of the possible applications of such models, also known as Born machines, is probabilistic inference, which is at the core of Bayesian methods. This paper studies the use of Born machines for the problem of training binary Bayesian neural networks. In the proposed approach, a Born machine is used to model the variational distribution of the binary weights of the neural network, and data from multiple tasks is used to reduce training data requirements on new tasks. The method combines gradient-based meta-learning and variational inference via Born machines, and is shown in a prototypical regression problem to outperform conventional joint learning strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge