Rule-based Data Selection for Large Language Models

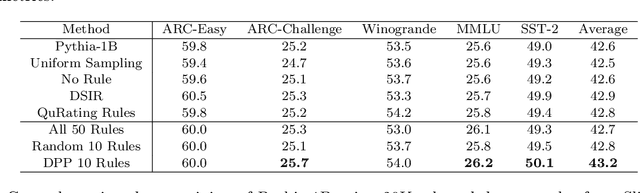
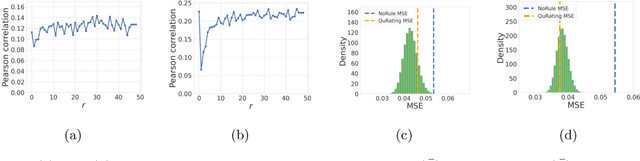
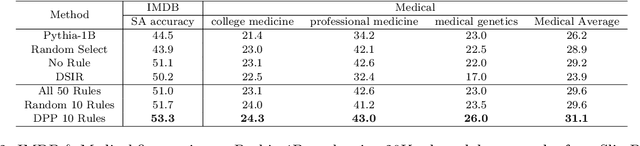
The quality of training data significantly impacts the performance of large language models (LLMs). There are increasing studies using LLMs to rate and select data based on several human-crafted metrics (rules). However, these conventional rule-based approaches often depend too heavily on human heuristics, lack effective metrics for assessing rules, and exhibit limited adaptability to new tasks. In our study, we introduce an innovative rule-based framework that utilizes the orthogonality of score vectors associated with rules as a novel metric for rule evaluations. Our approach includes an automated pipeline that first uses LLMs to generate a diverse set of rules, encompassing various rating dimensions to evaluate data quality. Then it rates a batch of data based on these rules and uses the determinantal point process (DPP) from random matrix theory to select the most orthogonal score vectors, thereby identifying a set of independent rules. These rules are subsequently used to evaluate all data, selecting samples with the highest average scores for downstream tasks such as LLM training. We verify the effectiveness of our method through two experimental setups: 1) comparisons with ground truth ratings and 2) benchmarking LLMs trained with the chosen data. Our comprehensive experiments cover a range of scenarios, including general pre-training and domain-specific fine-tuning in areas such as IMDB, Medical, Math, and Code. The outcomes demonstrate that our DPP-based rule rating method consistently outperforms other approaches, including rule-free rating, uniform sampling, importance resampling, and QuRating, in terms of both rating precision and model performance.

Asymptotics of Random Feature Regression Beyond the Linear Scaling Regime

Recent advances in machine learning have been achieved by using overparametrized models trained until near interpolation of the training data. It was shown, e.g., through the double descent phenomenon, that the number of parameters is a poor proxy for the model complexity and generalization capabilities. This leaves open the question of understanding the impact of parametrization on the performance of these models. How does model complexity and generalization depend on the number of parameters $p$? How should we choose $p$ relative to the sample size $n$ to achieve optimal test error? In this paper, we investigate the example of random feature ridge regression (RFRR). This model can be seen either as a finite-rank approximation to kernel ridge regression (KRR), or as a simplified model for neural networks trained in the so-called lazy regime. We consider covariates uniformly distributed on the $d$-dimensional sphere and compute sharp asymptotics for the RFRR test error in the high-dimensional polynomial scaling, where $p,n,d \to \infty$ while $p/ d^{\kappa_1}$ and $n / d^{\kappa_2}$ stay constant, for all $\kappa_1 , \kappa_2 \in \mathbb{R}_{>0}$. These asymptotics precisely characterize the impact of the number of random features and regularization parameter on the test performance. In particular, RFRR exhibits an intuitive trade-off between approximation and generalization power. For $n = o(p)$, the sample size $n$ is the bottleneck and RFRR achieves the same performance as KRR (which is equivalent to taking $p = \infty$). On the other hand, if $p = o(n)$, the number of random features $p$ is the limiting factor and RFRR test error matches the approximation error of the random feature model class (akin to taking $n = \infty$). Finally, a double descent appears at $n= p$, a phenomenon that was previously only characterized in the linear scaling $\kappa_1 = \kappa_2 = 1$.

Statistical Mechanics of Generalization In Graph Convolution Networks

Graph neural networks (GNN) have become the default machine learning model for relational datasets, including protein interaction networks, biological neural networks, and scientific collaboration graphs. We use tools from statistical physics and random matrix theory to precisely characterize generalization in simple graph convolution networks on the contextual stochastic block model. The derived curves are phenomenologically rich: they explain the distinction between learning on homophilic and heterophilic graphs and they predict double descent whose existence in GNNs has been questioned by recent work. Our results are the first to accurately explain the behavior not only of a stylized graph learning model but also of complex GNNs on messy real-world datasets. To wit, we use our analytic insights about homophily and heterophily to improve performance of state-of-the-art graph neural networks on several heterophilic benchmarks by a simple addition of negative self-loop filters.

Sharp Asymptotics of Kernel Ridge Regression Beyond the Linear Regime

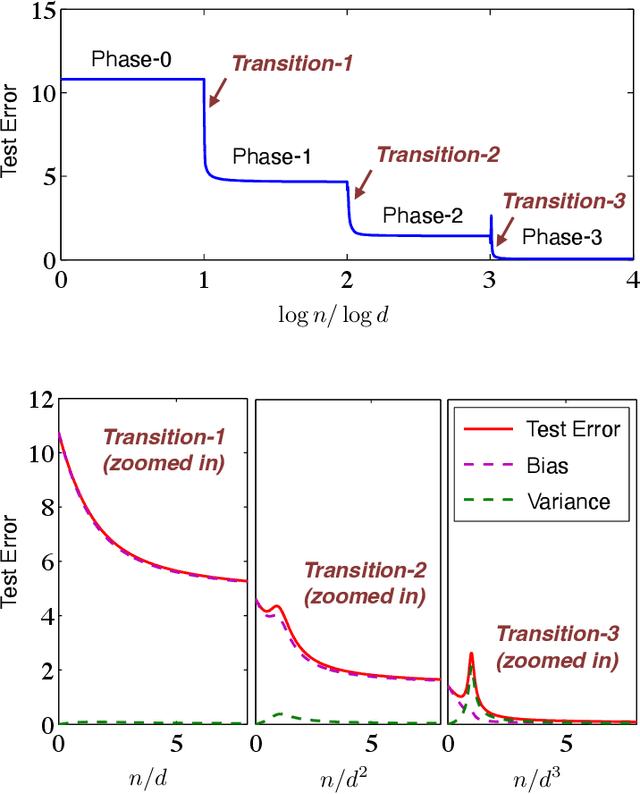
The generalization performance of kernel ridge regression (KRR) exhibits a multi-phased pattern that crucially depends on the scaling relationship between the sample size $n$ and the underlying dimension $d$. This phenomenon is due to the fact that KRR sequentially learns functions of increasing complexity as the sample size increases; when $d^{k-1}\ll n\ll d^{k}$, only polynomials with degree less than $k$ are learned. In this paper, we present sharp asymptotic characterization of the performance of KRR at the critical transition regions with $n \asymp d^k$, for $k\in\mathbb{Z}^{+}$. Our asymptotic characterization provides a precise picture of the whole learning process and clarifies the impact of various parameters (including the choice of the kernel function) on the generalization performance. In particular, we show that the learning curves of KRR can have a delicate "double descent" behavior due to specific bias-variance trade-offs at different polynomial scaling regimes.

Joint COCO and Mapillary Workshop at ICCV 2019 Keypoint Detection Challenge Track Technical Report: Distribution-Aware Coordinate Representation for Human Pose Estimation

In this paper, we focus on the coordinate representation in human pose estimation. While being the standard choice, heatmap based representation has not been systematically investigated. We found that the process of coordinate decoding (i.e. transforming the predicted heatmaps to the coordinates) is surprisingly significant for human pose estimation performance, which nevertheless was not recognised before. In light of the discovered importance, we further probe the design limitations of the standard coordinate decoding method and propose a principled distribution-aware decoding method. Meanwhile, we improve the standard coordinate encoding process (i.e. transforming ground-truth coordinates to heatmaps) by generating accurate heatmap distributions for unbiased model training. Taking them together, we formulate a novel Distribution-Aware coordinate Representation for Keypoint (DARK) method. Serving as a model-agnostic plug-in, DARK significantly improves the performance of a variety of state-of-the-art human pose estimation models. Extensive experiments show that DARK yields the best results on COCO keypoint detection challenge, validating the usefulness and effectiveness of our novel coordinate representation idea. The project page containing more details is at https://ilovepose.github.io/coco

A Solvable High-Dimensional Model of GAN

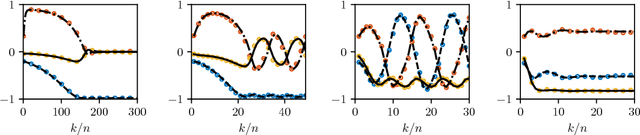
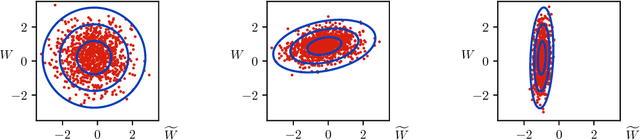
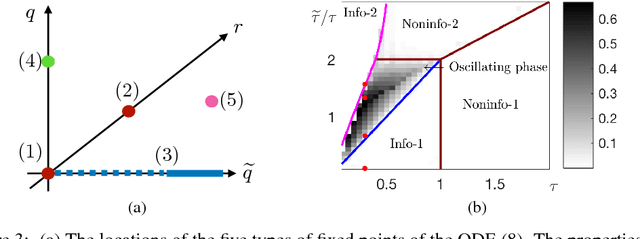
Despite the remarkable successes of generative adversarial networks (GANs) in many applications, theoretical understandings of their performance is still limited. In this paper, we present a simple shallow GAN model fed by high-dimensional input data. The dynamics of the training process of the proposed model can be exactly analyzed in the high-dimensional limit. In particular, by using the tool of scaling limits of stochastic processes, we show that the macroscopic quantities measuring the quality of the training process converge to a deterministic process that is characterized as the unique solution of a finite-dimensional ordinary differential equation (ODE). The proposed model is simple, but its training process already exhibits several different phases that can mimic the behaviors of more realistic GAN models used in practice. Specifically, depending on the choice of the learning rates, the training process can reach either a successful, a failed, or an oscillating phase. By studying the steady-state solutions of the limiting ODEs, we obtain a phase diagram that precisely characterizes the conditions under which each phase takes place. Although this work focuses on a simple GAN model, the analysis methods developed here might prove useful in the theoretical understanding of other variants of GANs with more advanced training algorithms.