A spring-block theory of feature learning in deep neural networks

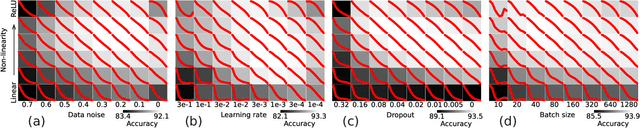
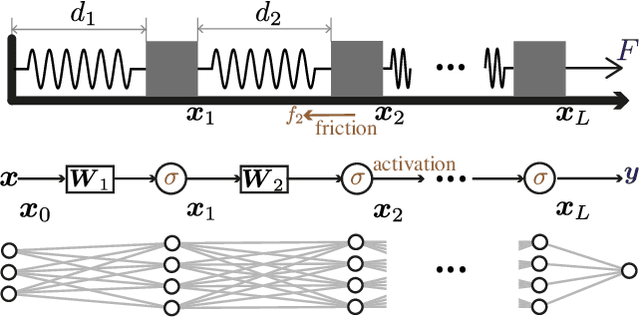
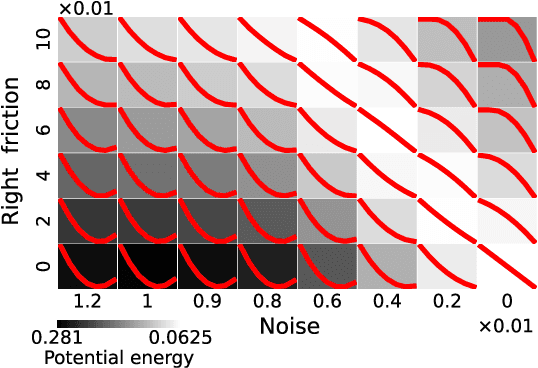
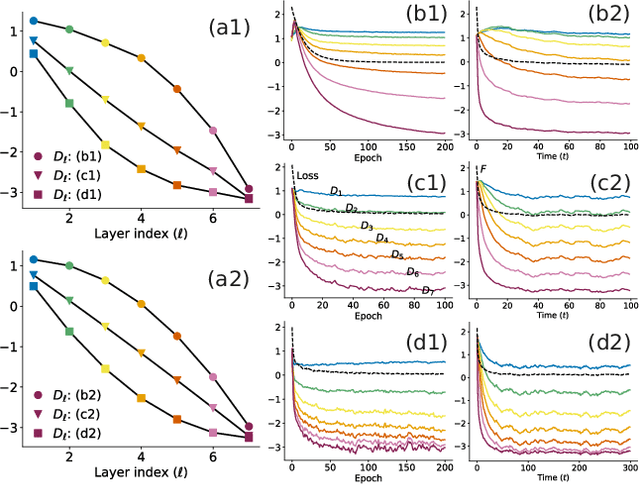
A central question in deep learning is how deep neural networks (DNNs) learn features. DNN layers progressively collapse data into a regular low-dimensional geometry. This collective effect of non-linearity, noise, learning rate, width, depth, and numerous other parameters, has eluded first-principles theories which are built from microscopic neuronal dynamics. Here we present a noise-non-linearity phase diagram that highlights where shallow or deep layers learn features more effectively. We then propose a macroscopic mechanical theory of feature learning that accurately reproduces this phase diagram, offering a clear intuition for why and how some DNNs are ``lazy'' and some are ``active'', and relating the distribution of feature learning over layers with test accuracy.

A Dynamical Graph Prior for Relational Inference

Relational inference aims to identify interactions between parts of a dynamical system from the observed dynamics. Current state-of-the-art methods fit a graph neural network (GNN) on a learnable graph to the dynamics. They use one-step message-passing GNNs -- intuitively the right choice since non-locality of multi-step or spectral GNNs may confuse direct and indirect interactions. But the \textit{effective} interaction graph depends on the sampling rate and it is rarely localized to direct neighbors, leading to local minima for the one-step model. In this work, we propose a \textit{dynamical graph prior} (DYGR) for relational inference. The reason we call it a prior is that, contrary to established practice, it constructively uses error amplification in high-degree non-local polynomial filters to generate good gradients for graph learning. To deal with non-uniqueness, DYGR simultaneously fits a ``shallow'' one-step model with shared graph topology. Experiments show that DYGR reconstructs graphs far more accurately than earlier methods, with remarkable robustness to under-sampling. Since appropriate sampling rates for unknown dynamical systems are not known a priori, this robustness makes DYGR suitable for real applications in scientific machine learning.

Statistical Mechanics of Generalization In Graph Convolution Networks

Graph neural networks (GNN) have become the default machine learning model for relational datasets, including protein interaction networks, biological neural networks, and scientific collaboration graphs. We use tools from statistical physics and random matrix theory to precisely characterize generalization in simple graph convolution networks on the contextual stochastic block model. The derived curves are phenomenologically rich: they explain the distinction between learning on homophilic and heterophilic graphs and they predict double descent whose existence in GNNs has been questioned by recent work. Our results are the first to accurately explain the behavior not only of a stylized graph learning model but also of complex GNNs on messy real-world datasets. To wit, we use our analytic insights about homophily and heterophily to improve performance of state-of-the-art graph neural networks on several heterophilic benchmarks by a simple addition of negative self-loop filters.

Neural Link Prediction with Walk Pooling

Graph neural networks achieve high accuracy in link prediction by jointly leveraging graph topology and node attributes. Topology, however, is represented indirectly; state-of-the-art methods based on subgraph classification label nodes with distance to the target link, so that, although topological information is present, it is tempered by pooling. This makes it challenging to leverage features like loops and motifs associated with network formation mechanisms. We propose a link prediction algorithm based on a new pooling scheme called WalkPool. WalkPool combines the expressivity of topological heuristics with the feature-learning ability of neural networks. It summarizes a putative link by random walk probabilities of adjacent paths. Instead of extracting transition probabilities from the original graph, it computes the transition matrix of a "predictive" latent graph by applying attention to learned features; this may be interpreted as feature-sensitive topology fingerprinting. WalkPool can leverage unsupervised node features or be combined with GNNs and trained end-to-end. It outperforms state-of-the-art methods on all common link prediction benchmarks, both homophilic and heterophilic, with and without node attributes. Applying WalkPool to a set of unsupervised GNNs significantly improves prediction accuracy, suggesting that it may be used as a general-purpose graph pooling scheme.

Link Prediction via Matrix Completion

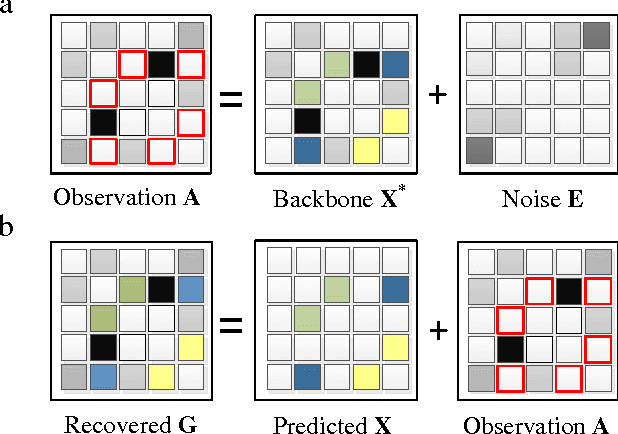
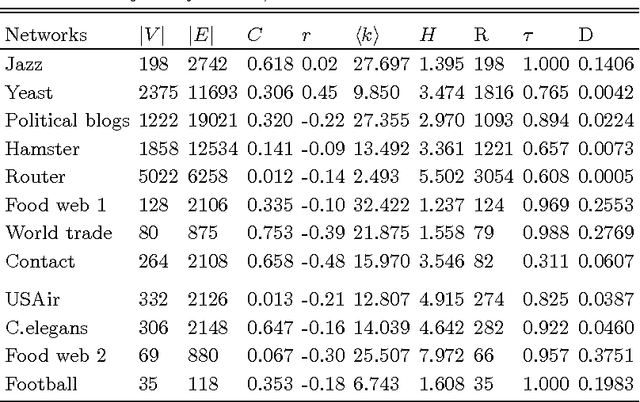
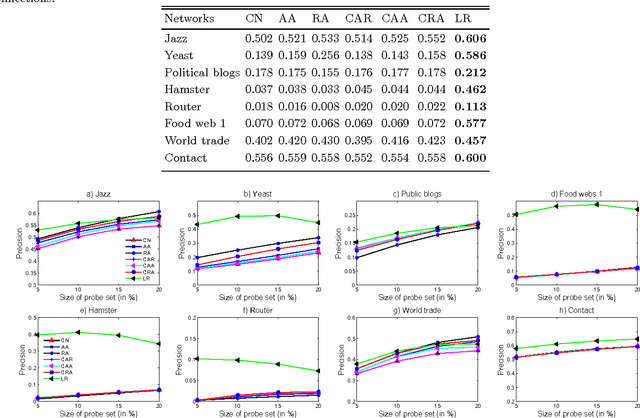
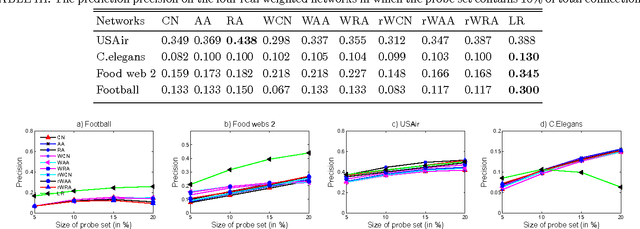
Inspired by practical importance of social networks, economic networks, biological networks and so on, studies on large and complex networks have attracted a surge of attentions in the recent years. Link prediction is a fundamental issue to understand the mechanisms by which new links are added to the networks. We introduce the method of robust principal component analysis (robust PCA) into link prediction, and estimate the missing entries of the adjacency matrix. On one hand, our algorithm is based on the sparsity and low rank property of the matrix, on the other hand, it also performs very well when the network is dense. This is because a relatively dense real network is also sparse in comparison to the complete graph. According to extensive experiments on real networks from disparate fields, when the target network is connected and sufficiently dense, whatever it is weighted or unweighted, our method is demonstrated to be very effective and with prediction accuracy being considerably improved comparing with many state-of-the-art algorithms.