Sharp Asymptotics of Kernel Ridge Regression Beyond the Linear Regime
Paper and Code
May 13, 2022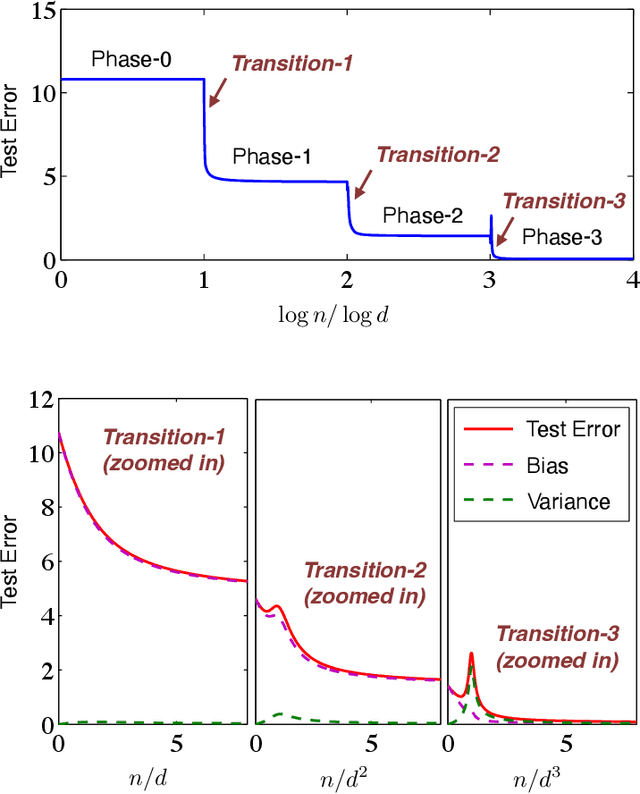
The generalization performance of kernel ridge regression (KRR) exhibits a multi-phased pattern that crucially depends on the scaling relationship between the sample size $n$ and the underlying dimension $d$. This phenomenon is due to the fact that KRR sequentially learns functions of increasing complexity as the sample size increases; when $d^{k-1}\ll n\ll d^{k}$, only polynomials with degree less than $k$ are learned. In this paper, we present sharp asymptotic characterization of the performance of KRR at the critical transition regions with $n \asymp d^k$, for $k\in\mathbb{Z}^{+}$. Our asymptotic characterization provides a precise picture of the whole learning process and clarifies the impact of various parameters (including the choice of the kernel function) on the generalization performance. In particular, we show that the learning curves of KRR can have a delicate "double descent" behavior due to specific bias-variance trade-offs at different polynomial scaling regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge