ScRAE: Deterministic Regularized Autoencoders with Flexible Priors for Clustering Single-cell Gene Expression Data

Clustering single-cell RNA sequence (scRNA-seq) data poses statistical and computational challenges due to their high-dimensionality and data-sparsity, also known as `dropout' events. Recently, Regularized Auto-Encoder (RAE) based deep neural network models have achieved remarkable success in learning robust low-dimensional representations. The basic idea in RAEs is to learn a non-linear mapping from the high-dimensional data space to a low-dimensional latent space and vice-versa, simultaneously imposing a distributional prior on the latent space, which brings in a regularization effect. This paper argues that RAEs suffer from the infamous problem of bias-variance trade-off in their naive formulation. While a simple AE without a latent regularization results in data over-fitting, a very strong prior leads to under-representation and thus bad clustering. To address the above issues, we propose a modified RAE framework (called the scRAE) for effective clustering of the single-cell RNA sequencing data. scRAE consists of deterministic AE with a flexibly learnable prior generator network, which is jointly trained with the AE. This facilitates scRAE to trade-off better between the bias and variance in the latent space. We demonstrate the efficacy of the proposed method through extensive experimentation on several real-world single-cell Gene expression datasets.

A Unified Framework for Generic, Query-Focused, Privacy Preserving and Update Summarization using Submodular Information Measures

We study submodular information measures as a rich framework for generic, query-focused, privacy sensitive, and update summarization tasks. While past work generally treats these problems differently ({\em e.g.}, different models are often used for generic and query-focused summarization), the submodular information measures allow us to study each of these problems via a unified approach. We first show that several previous query-focused and update summarization techniques have, unknowingly, used various instantiations of the aforesaid submodular information measures, providing evidence for the benefit and naturalness of these models. We then carefully study and demonstrate the modelling capabilities of the proposed functions in different settings and empirically verify our findings on both a synthetic dataset and an existing real-world image collection dataset (that has been extended by adding concept annotations to each image making it suitable for this task) and will be publicly released. We employ a max-margin framework to learn a mixture model built using the proposed instantiations of submodular information measures and demonstrate the effectiveness of our approach. While our experiments are in the context of image summarization, our framework is generic and can be easily extended to other summarization settings (e.g., videos or documents).

Submodular Combinatorial Information Measures with Applications in Machine Learning

Information-theoretic quantities like entropy and mutual information have found numerous uses in machine learning. It is well known that there is a strong connection between these entropic quantities and submodularity since entropy over a set of random variables is submodular. In this paper, we study combinatorial information measures that generalize independence, (conditional) entropy, (conditional) mutual information, and total correlation defined over sets of (not necessarily random) variables. These measures strictly generalize the corresponding entropic measures since they are all parameterized via submodular functions that themselves strictly generalize entropy. Critically, we show that, unlike entropic mutual information in general, the submodular mutual information is actually submodular in one argument, holding the other fixed, for a large class of submodular functions whose third-order partial derivatives satisfy a non-negativity property. This turns out to include a number of practically useful cases such as the facility location and set-cover functions. We study specific instantiations of the submodular information measures on these, as well as the probabilistic coverage, graph-cut, and saturated coverage functions, and see that they all have mathematically intuitive and practically useful expressions. Regarding applications, we connect the maximization of submodular (conditional) mutual information to problems such as mutual-information-based, query-based, and privacy-preserving summarization -- and we connect optimizing the multi-set submodular mutual information to clustering and robust partitioning.

To Regularize or Not To Regularize? The Bias Variance Trade-off in Regularized AEs

Regularized Auto-Encoders (AE) form a rich class of methods within the landscape of neural generative models. They effectively model the joint-distribution between the data and a latent space using an Encoder-Decoder combination, with regularization imposed in terms of a prior over the latent space. Despite their advantages such as stability in training, the performance of AE based models has not reached that of the other models such as GANs. While several reasons including the presence of conflicting terms in the objective, distributional choices imposed on the Encoder and the Decoder, and dimensionality of the latent space have been identified as possible causes for the suboptimal performance, the role of the regularization (prior distribution) imposed has not been studied systematically. Motivated by this, we examine the effect of the latent prior on the generation quality of the AE models in this paper. We show that there is no single fixed prior which is optimal for all data distributions, given a Gaussian Decoder. Further, with finite data, we show that there exists a bias-variance trade-off that comes with prior imposition. As a remedy, we optimize a generalized ELBO objective, with an additional state space over the latent prior. We implicitly learn this flexible prior jointly with the AE training using an adversarial learning technique, which facilitates operation on different points of the bias-variance curve. Our experiments on multiple datasets show that the proposed method is the new state-of-the-art for AE based generative models.

C-MI-GAN : Estimation of Conditional Mutual Information using MinMax formulation

Estimation of information theoretic quantities such as mutual information and its conditional variant has drawn interest in recent times owing to their multifaceted applications. Newly proposed neural estimators for these quantities have overcome severe drawbacks of classical $k$NN-based estimators in high dimensions. In this work, we focus on conditional mutual information (CMI) estimation by utilizing its formulation as a minmax optimization problem. Such a formulation leads to a joint training procedure similar to that of generative adversarial networks. We find that our proposed estimator provides better estimates than the existing approaches on a variety of simulated data sets comprising linear and non-linear relations between variables. As an application of CMI estimation, we deploy our estimator for conditional independence (CI) testing on real data and obtain better results than state-of-the-art CI testers.

Towards Latent Space Optimality for Auto-Encoder Based Generative Models

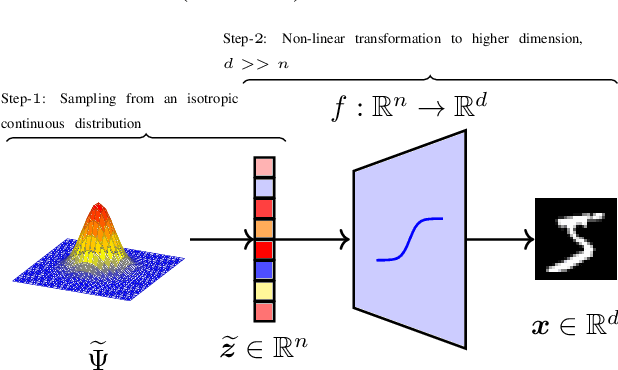
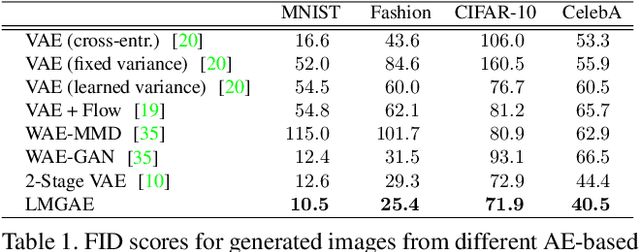
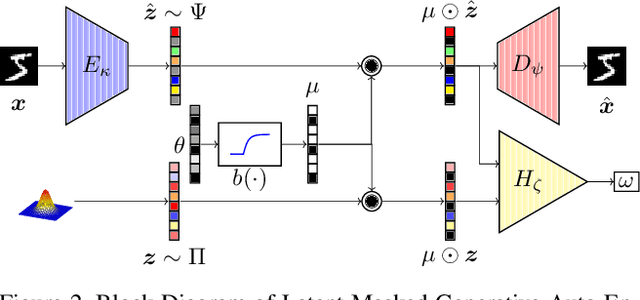
The field of neural generative models is dominated by the highly successful Generative Adversarial Networks (GANs) despite their challenges, such as training instability and mode collapse. Auto-Encoders (AE) with regularized latent space provides an alternative framework for generative models, albeit their performance levels have not reached that of GANs. In this work, we identify one of the causes for the under-performance of AE-based models and propose a remedial measure. Specifically, we hypothesize that the dimensionality of the AE model's latent space has a critical effect on the quality of the generated data. Under the assumption that nature generates data by sampling from a "true" generative latent space followed by a deterministic non-linearity, we show that the optimal performance is obtained when the dimensionality of the latent space of the AE-model matches with that of the "true" generative latent space. Further, we propose an algorithm called the Latent Masked Generative Auto-Encoder (LMGAE), in which the dimensionality of the model's latent space is brought closer to that of the "true" generative latent space, via a novel procedure to mask the spurious latent dimensions. We demonstrate through experiments on synthetic and several real-world datasets that the proposed formulation yields generation quality that is better than the state-of-the-art AE-based generative models and is comparable to that of GANs.

Turbo Autoencoder: Deep learning based channel codes for point-to-point communication channels

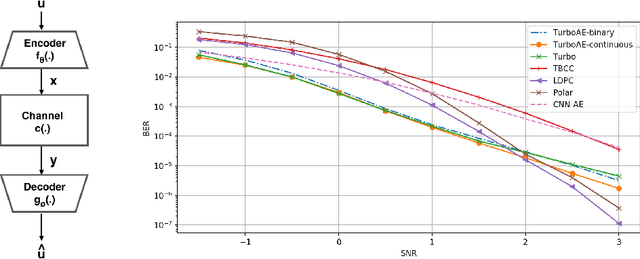
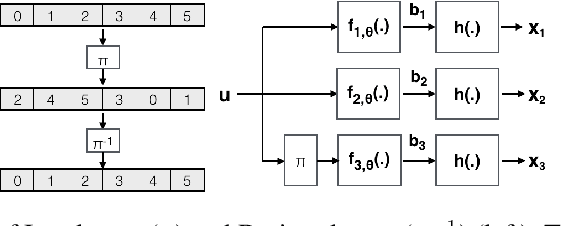
Designing codes that combat the noise in a communication medium has remained a significant area of research in information theory as well as wireless communications. Asymptotically optimal channel codes have been developed by mathematicians for communicating under canonical models after over 60 years of research. On the other hand, in many non-canonical channel settings, optimal codes do not exist and the codes designed for canonical models are adapted via heuristics to these channels and are thus not guaranteed to be optimal. In this work, we make significant progress on this problem by designing a fully end-to-end jointly trained neural encoder and decoder, namely, Turbo Autoencoder (TurboAE), with the following contributions: ($a$) under moderate block lengths, TurboAE approaches state-of-the-art performance under canonical channels; ($b$) moreover, TurboAE outperforms the state-of-the-art codes under non-canonical settings in terms of reliability. TurboAE shows that the development of channel coding design can be automated via deep learning, with near-optimal performance.

CCMI : Classifier based Conditional Mutual Information Estimation

Conditional Mutual Information (CMI) is a measure of conditional dependence between random variables X and Y, given another random variable Z. It can be used to quantify conditional dependence among variables in many data-driven inference problems such as graphical models, causal learning, feature selection and time-series analysis. While k-nearest neighbor (kNN) based estimators as well as kernel-based methods have been widely used for CMI estimation, they suffer severely from the curse of dimensionality. In this paper, we leverage advances in classifiers and generative models to design methods for CMI estimation. Specifically, we introduce an estimator for KL-Divergence based on the likelihood ratio by training a classifier to distinguish the observed joint distribution from the product distribution. We then show how to construct several CMI estimators using this basic divergence estimator by drawing ideas from conditional generative models. We demonstrate that the estimates from our proposed approaches do not degrade in performance with increasing dimension and obtain significant improvement over the widely used KSG estimator. Finally, as an application of accurate CMI estimation, we use our best estimator for conditional independence testing and achieve superior performance than the state-of-the-art tester on both simulated and real data-sets.

LEARN Codes: Inventing Low-latency Codes via Recurrent Neural Networks

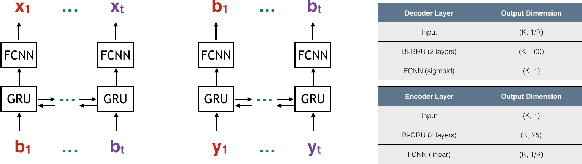
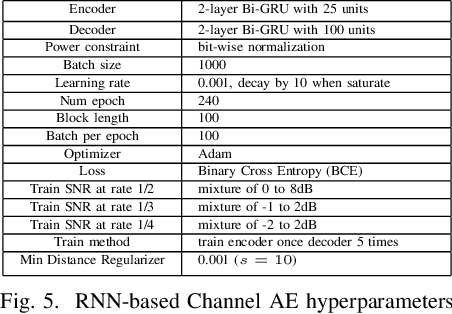
Designing channel codes under low latency constraints is one of the most demanding requirements in 5G standards. However, sharp characterizations of the performances of traditional codes are only available in the large block-length limit. Code designs are guided by those asymptotic analyses and require large block lengths and long latency to achieve the desired error rate. Furthermore, when the codes designed for one channel (e.g. Additive White Gaussian Noise (AWGN) channel) are used for another (e.g. non-AWGN channels), heuristics are necessary to achieve any nontrivial performance -thereby severely lacking in robustness as well as adaptivity. Obtained by jointly designing Recurrent Neural Network (RNN) based encoder and decoder, we propose an end-to-end learned neural code which outperforms canonical convolutional code under block settings. With this gained experience of designing a novel neural block code, we propose a new class of codes under low latency constraint - Low-latency Efficient Adaptive Robust Neural (LEARN) codes, which outperforms the state-of-the-art low latency codes as well as exhibits robustness and adaptivity properties. LEARN codes show the potential of designing new versatile and universal codes for future communications via tools of modern deep learning coupled with communication engineering insights.

ClusterGAN : Latent Space Clustering in Generative Adversarial Networks

Generative Adversarial networks (GANs) have obtained remarkable success in many unsupervised learning tasks and unarguably, clustering is an important unsupervised learning problem. While one can potentially exploit the latent-space back-projection in GANs to cluster, we demonstrate that the cluster structure is not retained in the GAN latent space. In this paper, we propose ClusterGAN as a new mechanism for clustering using GANs. By sampling latent variables from a mixture of one-hot encoded variables and continuous latent variables, coupled with an inverse network (which projects the data to the latent space) trained jointly with a clustering specific loss, we are able to achieve clustering in the latent space. Our results show a remarkable phenomenon that GANs can preserve latent space interpolation across categories, even though the discriminator is never exposed to such vectors. We compare our results with various clustering baselines and demonstrate superior performance on both synthetic and real datasets.