Hengfa Lu
Accelerated MR Fingerprinting with Low-Rank and Generative Subspace Modeling
May 25, 2023



Abstract:Magnetic Resonance (MR) Fingerprinting is an emerging multi-parametric quantitative MR imaging technique, for which image reconstruction methods utilizing low-rank and subspace constraints have achieved state-of-the-art performance. However, this class of methods often suffers from an ill-conditioned model-fitting issue, which degrades the performance as the data acquisition lengths become short and/or the signal-to-noise ratio becomes low. To address this problem, we present a new image reconstruction method for MR Fingerprinting, integrating low-rank and subspace modeling with a deep generative prior. Specifically, the proposed method captures the strong spatiotemporal correlation of contrast-weighted time-series images in MR Fingerprinting via a low-rank factorization. Further, it utilizes an untrained convolutional generative neural network to represent the spatial subspace of the low-rank model, while estimating the temporal subspace of the model from simulated magnetization evolutions generated based on spin physics. Here the architecture of the generative neural network serves as an effective regularizer for the ill-conditioned inverse problem without additional spatial training data that are often expensive to acquire. The proposed formulation results in a non-convex optimization problem, for which we develop an algorithm based on variable splitting and alternating direction method of multipliers.We evaluate the performance of the proposed method with numerical simulations and in vivo experiments and demonstrate that the proposed method outperforms the state-of-the-art low-rank and subspace reconstruction.
Accelerated MRI Reconstruction with Separable and Enhanced Low-Rank Hankel Regularization
Jul 24, 2021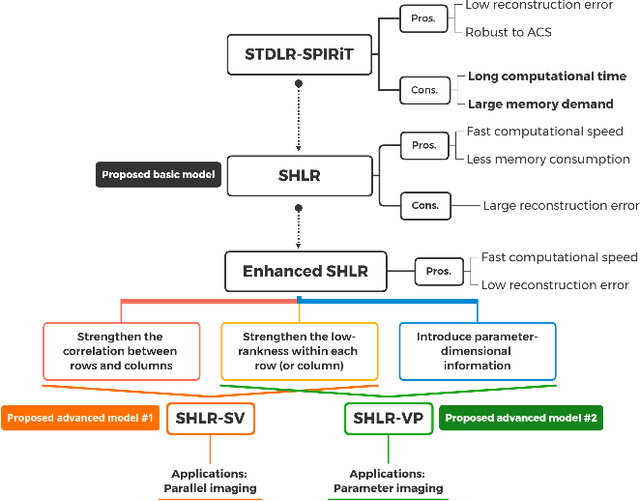
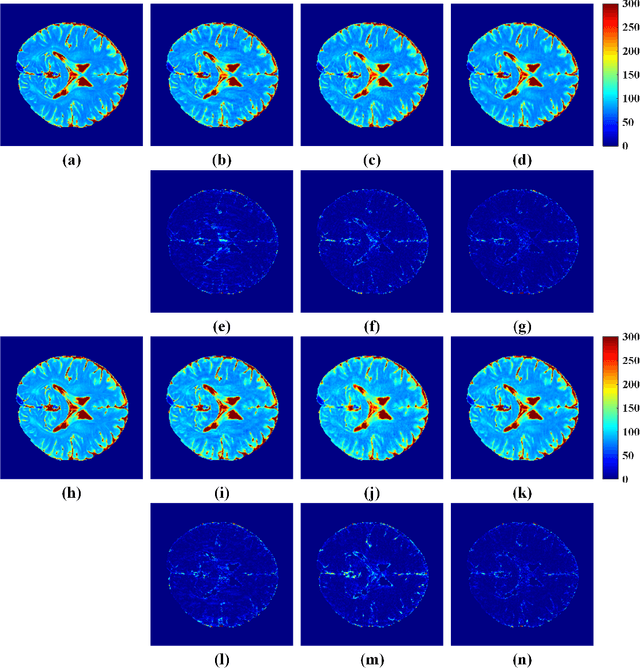
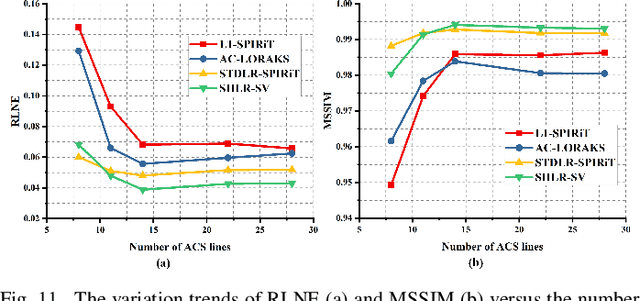

Abstract:The combination of the sparse sampling and the low-rank structured matrix reconstruction has shown promising performance, enabling a significant reduction of the magnetic resonance imaging data acquisition time. However, the low-rank structured approaches demand considerable memory consumption and are time-consuming due to a noticeable number of matrix operations performed on the huge-size block Hankel-like matrix. In this work, we proposed a novel framework to utilize the low-rank property but meanwhile to achieve faster reconstructions and promising results. The framework allows us to enforce the low-rankness of Hankel matrices constructing from 1D vectors instead of 2D matrices from 1D vectors and thus avoid the construction of huge block Hankel matrix for 2D k-space matrices. Moreover, under this framework, we can easily incorporate other information, such as the smooth phase of the image and the low-rankness in the parameter dimension, to further improve the image quality. We built and validated two models for parallel and parameter magnetic resonance imaging experiments, respectively. Our retrospective in-vivo results indicate that the proposed approaches enable faster reconstructions than the state-of-the-art approaches, e.g., about 8x faster than STDLRSPIRiT, and faithful removal of undersampling artifacts.
A Convergence Proof of Projected Fast Iterative Soft-thresholding Algorithm for Parallel Magnetic Resonance Imaging
Sep 17, 2019



Abstract:The boom of non-uniform sampling and compressed sensing techniques dramatically alleviates the prolonged data acquisition problem of magnetic resonance imaging. Sparse reconstruction, thanks to its fast computation and promising performance, has attracted researchers to put numerous efforts on it and has been adopted in commercial scanners. Algorithms for solving the sparse reconstruction models play an essential role in sparse reconstruction. Being a simple and efficient algorithm for sparse reconstruction, pFISTA has been successfully extended to parallel imaging, however, its convergence criterion is still an open question, confusing users on the setting of the parameter which assures the convergence of the algorithm. In this work, we prove the convergence of the parallel imaging version pFISTA. Specifically, the convergences of two well-known parallel imaging reconstruction models, SENSE and SPIRiT, solved by pFISTA are proved. Experiments on brain images demonstrate the validity of the convergence criterion. The convergence criterion proofed in this work can help users quickly obtain the satisfy parameter that admits faithful results and fast convergence speeds.
Accelerated Nuclear Magnetic Resonance Spectroscopy with Deep Learning
May 14, 2019
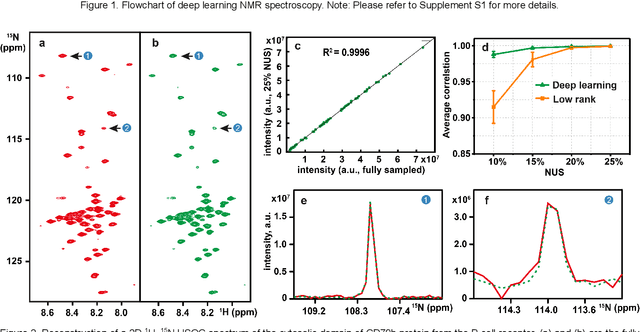
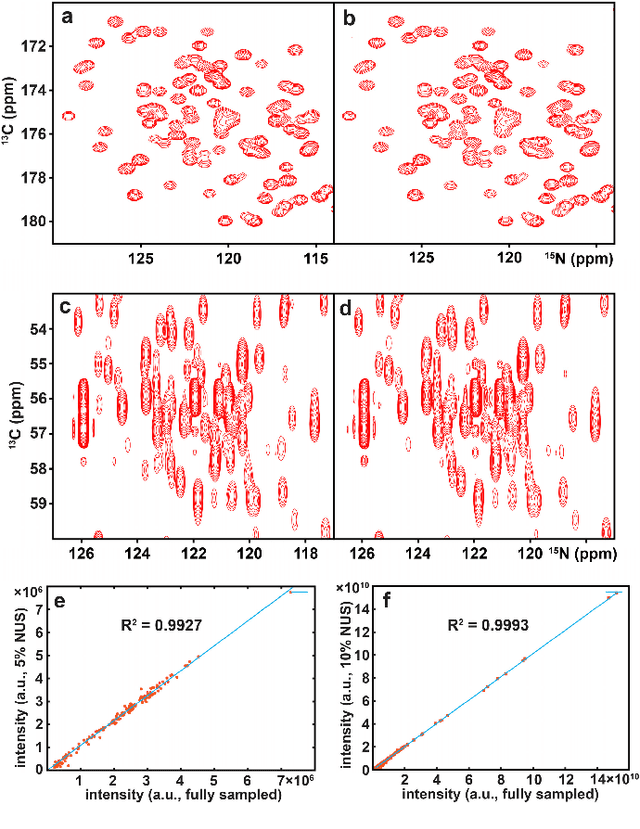

Abstract:Nuclear magnetic resonance (NMR) spectroscopy serves as an indispensable tool in chemistry and biology but often suffers from long experimental time. We present a proof-of-concept of application of deep learning and neural network for high-quality, reliable, and very fast NMR spectra reconstruction from limited experimental data. We show that the neural network training can be achieved using solely synthetic NMR signal, which lifts the prohibiting demand for a large volume of realistic training data usually required in the deep learning approach.
Hankel Matrix Nuclear Norm Regularized Tensor Completion for $N$-dimensional Exponential Signals
Mar 31, 2017



Abstract:Signals are generally modeled as a superposition of exponential functions in spectroscopy of chemistry, biology and medical imaging. For fast data acquisition or other inevitable reasons, however, only a small amount of samples may be acquired and thus how to recover the full signal becomes an active research topic. But existing approaches can not efficiently recover $N$-dimensional exponential signals with $N\geq 3$. In this paper, we study the problem of recovering N-dimensional (particularly $N\geq 3$) exponential signals from partial observations, and formulate this problem as a low-rank tensor completion problem with exponential factor vectors. The full signal is reconstructed by simultaneously exploiting the CANDECOMP/PARAFAC structure and the exponential structure of the associated factor vectors. The latter is promoted by minimizing an objective function involving the nuclear norm of Hankel matrices. Experimental results on simulated and real magnetic resonance spectroscopy data show that the proposed approach can successfully recover full signals from very limited samples and is robust to the estimated tensor rank.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge