Zongying Lai
Accelerated MRI Reconstruction with Separable and Enhanced Low-Rank Hankel Regularization
Jul 24, 2021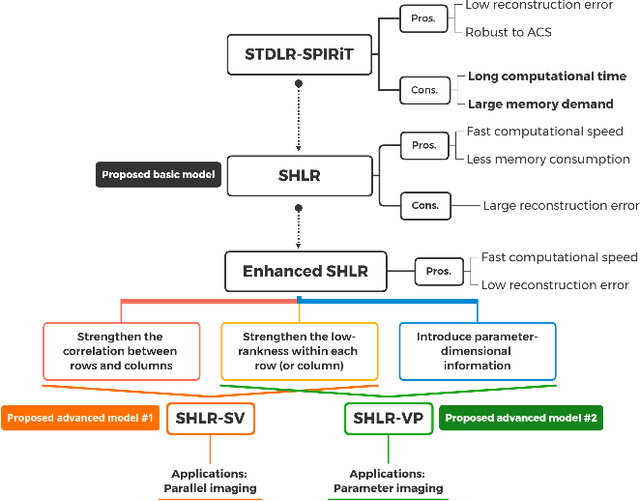
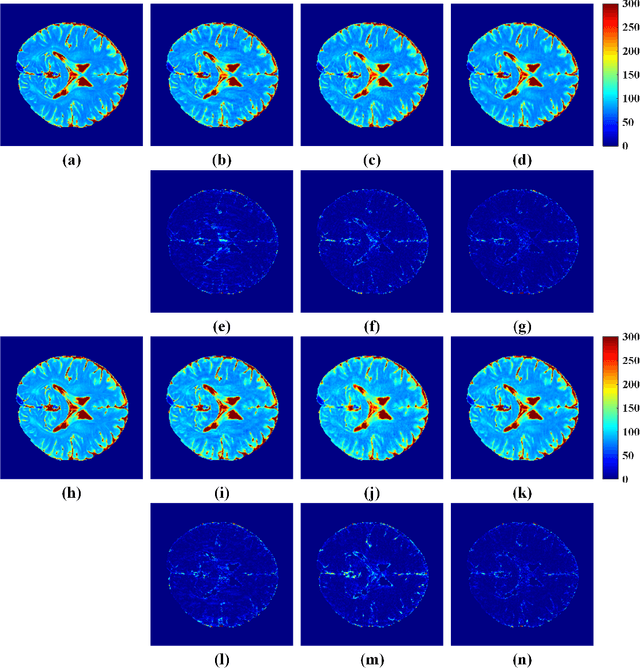
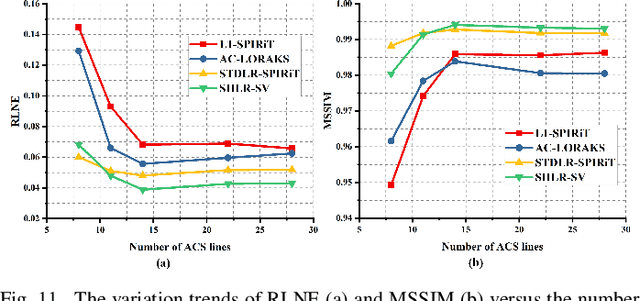

Abstract:The combination of the sparse sampling and the low-rank structured matrix reconstruction has shown promising performance, enabling a significant reduction of the magnetic resonance imaging data acquisition time. However, the low-rank structured approaches demand considerable memory consumption and are time-consuming due to a noticeable number of matrix operations performed on the huge-size block Hankel-like matrix. In this work, we proposed a novel framework to utilize the low-rank property but meanwhile to achieve faster reconstructions and promising results. The framework allows us to enforce the low-rankness of Hankel matrices constructing from 1D vectors instead of 2D matrices from 1D vectors and thus avoid the construction of huge block Hankel matrix for 2D k-space matrices. Moreover, under this framework, we can easily incorporate other information, such as the smooth phase of the image and the low-rankness in the parameter dimension, to further improve the image quality. We built and validated two models for parallel and parameter magnetic resonance imaging experiments, respectively. Our retrospective in-vivo results indicate that the proposed approaches enable faster reconstructions than the state-of-the-art approaches, e.g., about 8x faster than STDLRSPIRiT, and faithful removal of undersampling artifacts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge