A Faithful Deep Sensitivity Estimation for Accelerated Magnetic Resonance Imaging

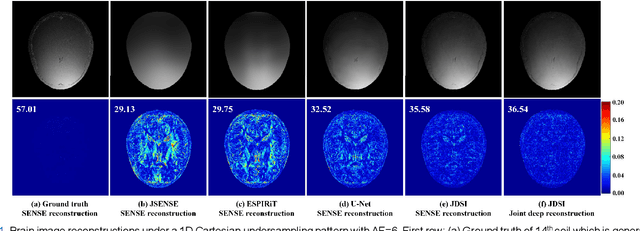
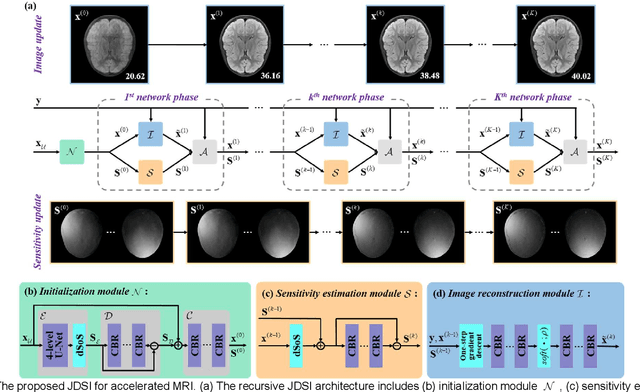
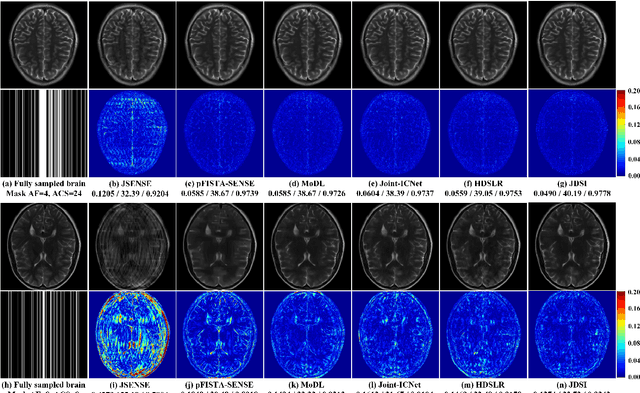
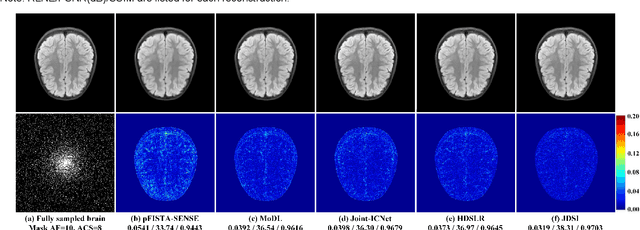
Recent deep learning is superior in providing high-quality images and ultra-fast reconstructions in accelerated magnetic resonance imaging (MRI). Faithful coil sensitivity estimation is vital for MRI reconstruction. However, most deep learning methods still rely on pre-estimated sensitivity maps and ignore their inaccuracy, resulting in the significant quality degradation of reconstructed images. In this work, we propose a Joint Deep Sensitivity estimation and Image reconstruction network, called JDSI. During the image artifacts removal, it gradually provides more faithful sensitivity maps, leading to greatly improved image reconstructions. To understand the behavior of the network, the mutual promotion of sensitivity estimation and image reconstruction is revealed through the visualization of network intermediate results. Results on in vivo datasets and radiologist reader study demonstrate that, the proposed JDSI achieves the state-of-the-art performance visually and quantitatively, especially when the accelerated factor is high. Additionally, JDSI owns nice robustness to abnormal subjects and different number of autocalibration signals.

pISTA-SENSE-ResNet for Parallel MRI Reconstruction

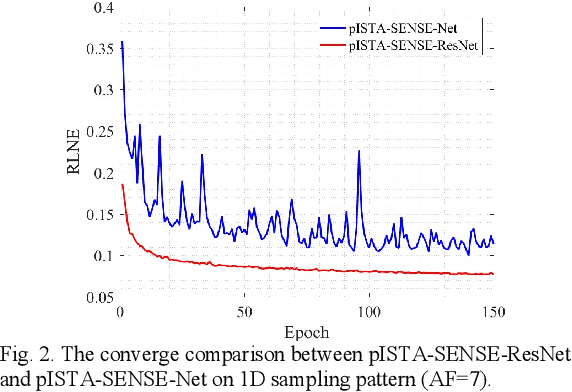
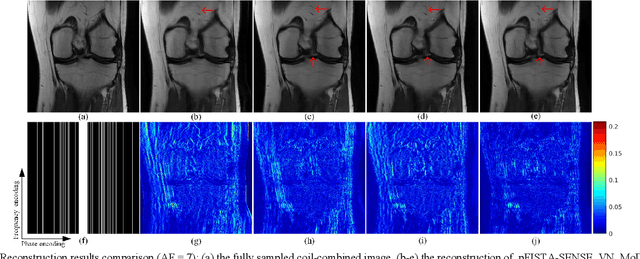
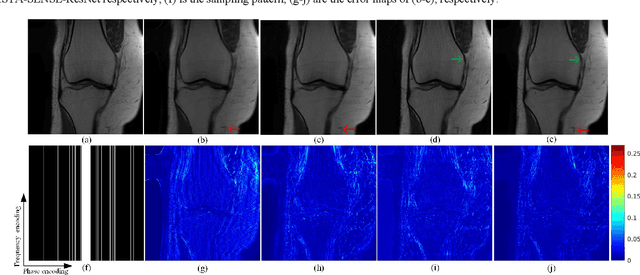
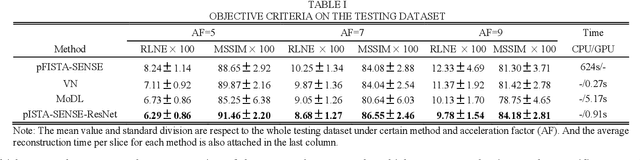
Magnetic resonance imaging has been widely applied in clinical diagnosis, however, is limited by its long data acquisition time. Although imaging can be accelerated by sparse sampling and parallel imaging, achieving promising reconstruction images with a fast reconstruction speed remains a challenge. Recently, deep learning approaches have attracted a lot of attention for its encouraging reconstruction results but without a proper interpretability. In this letter, to enable high-quality image reconstruction for the parallel magnetic resonance imaging, we design the network structure from the perspective of sparse iterative reconstruction and enhance it with the residual structure. The experimental results of a public knee dataset show that compared with the optimization-based method and the latest deep learning parallel imaging methods, the proposed network has less error in reconstruction and is more stable under different acceleration factors.

A Convergence Proof of Projected Fast Iterative Soft-thresholding Algorithm for Parallel Magnetic Resonance Imaging

The boom of non-uniform sampling and compressed sensing techniques dramatically alleviates the prolonged data acquisition problem of magnetic resonance imaging. Sparse reconstruction, thanks to its fast computation and promising performance, has attracted researchers to put numerous efforts on it and has been adopted in commercial scanners. Algorithms for solving the sparse reconstruction models play an essential role in sparse reconstruction. Being a simple and efficient algorithm for sparse reconstruction, pFISTA has been successfully extended to parallel imaging, however, its convergence criterion is still an open question, confusing users on the setting of the parameter which assures the convergence of the algorithm. In this work, we prove the convergence of the parallel imaging version pFISTA. Specifically, the convergences of two well-known parallel imaging reconstruction models, SENSE and SPIRiT, solved by pFISTA are proved. Experiments on brain images demonstrate the validity of the convergence criterion. The convergence criterion proofed in this work can help users quickly obtain the satisfy parameter that admits faithful results and fast convergence speeds.