Real-Time Energy-Optimal Path Planning for Electric Vehicles

The rapid adoption of electric vehicles (EVs) in modern transport systems has made energy-aware routing a critical task in their successful integration, especially within large-scale networks. In cases where an EV's remaining energy is limited and charging locations are not easily accessible, some destinations may only be reachable through an energy-optimal path: a route that consumes less energy than all other alternatives. The feasibility of such energy-efficient paths depends heavily on the accuracy of the energy model used for planning, and thus failing to account for vehicle dynamics can lead to inaccurate energy estimates, rendering some planned routes infeasible in reality. This paper explores the impact of vehicle dynamics on energy-optimal path planning for EVs. We develop an accurate energy model that incorporates key vehicle dynamics parameters into energy calculations, thereby reducing the risk of planning infeasible paths under battery constraints. The paper also introduces two novel online reweighting functions that allow for a faster, pre-processing free, pathfinding in the presence of negative energy costs resulting from regenerative braking, making them ideal for real-time applications. Through extensive experimentation on real-world transport networks, we demonstrate that our approach considerably enhances energy-optimal pathfinding for EVs in both computational efficiency and energy estimation accuracy.

Comparison and Evaluation of Methods for a Predict+Optimize Problem in Renewable Energy

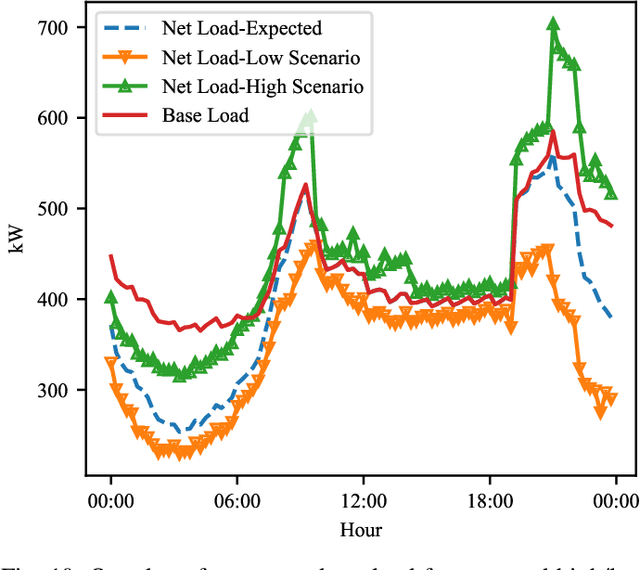
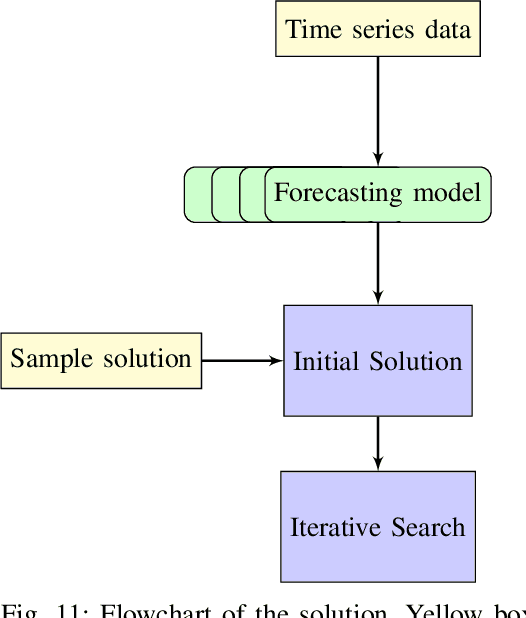
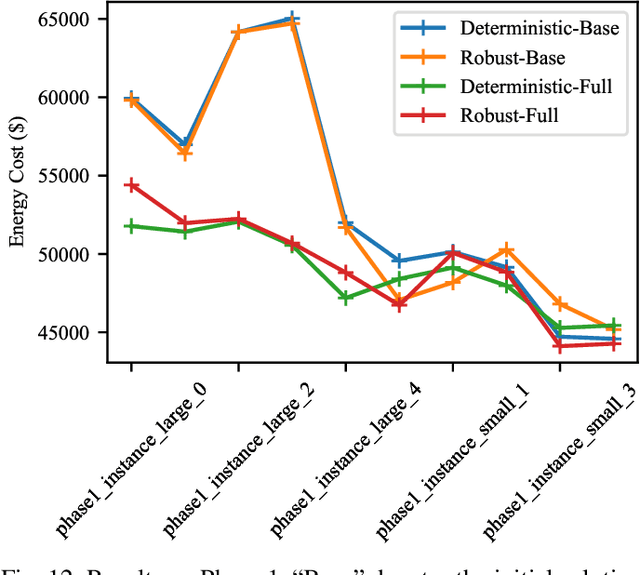
Algorithms that involve both forecasting and optimization are at the core of solutions to many difficult real-world problems, such as in supply chains (inventory optimization), traffic, and in the transition towards carbon-free energy generation in battery/load/production scheduling in sustainable energy systems. Typically, in these scenarios we want to solve an optimization problem that depends on unknown future values, which therefore need to be forecast. As both forecasting and optimization are difficult problems in their own right, relatively few research has been done in this area. This paper presents the findings of the ``IEEE-CIS Technical Challenge on Predict+Optimize for Renewable Energy Scheduling," held in 2021. We present a comparison and evaluation of the seven highest-ranked solutions in the competition, to provide researchers with a benchmark problem and to establish the state of the art for this benchmark, with the aim to foster and facilitate research in this area. The competition used data from the Monash Microgrid, as well as weather data and energy market data. It then focused on two main challenges: forecasting renewable energy production and demand, and obtaining an optimal schedule for the activities (lectures) and on-site batteries that lead to the lowest cost of energy. The most accurate forecasts were obtained by gradient-boosted tree and random forest models, and optimization was mostly performed using mixed integer linear and quadratic programming. The winning method predicted different scenarios and optimized over all scenarios jointly using a sample average approximation method.

Enhanced Methods for the Weight Constrained Shortest Path Problem: Constrained Path Finding Meets Bi-objective Search

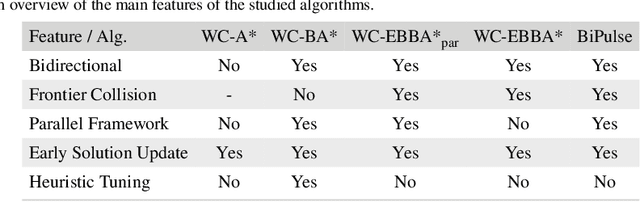
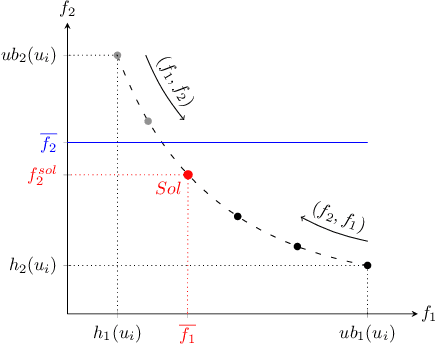
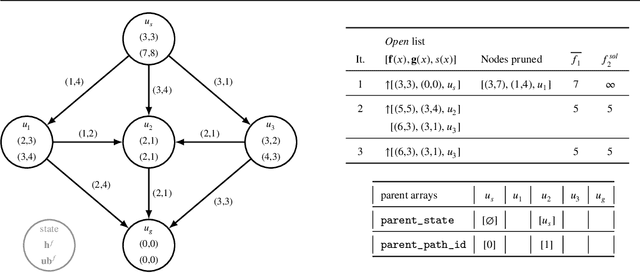
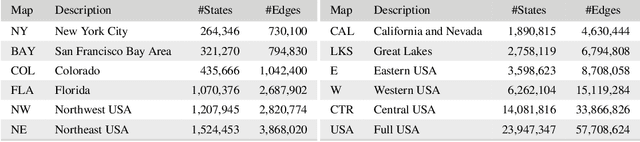
The classic problem of \textit{constrained path finding} is a well-studied but yet challenging topic in AI with a broad range of applications in various areas such communication and transportation. The Weight Constrained Shortest Path Problem (WCSPP), as the base form of constrained path finding with only one side constraint, aims to plan a cost optimum path whose weight/resource usage is limited. Given the bi-criteria nature of the problem (i.e., dealing with cost and weight of paths), methods addressing the WCSPP have some common properties with bi-objective search. This paper leverages the recent state-of-the-art A*-based techniques in both constrained path finding and bi-objective search and presents two exact solution approaches to the WCSPP, both capable of solving hard problem instances on very large graphs. We empirically evaluate the performance of our algorithms on a new set of large and realistic problem instances and show their advantages over the state-of-the-art algorithms in both time and space metrics. This paper also investigates the importance of priority queues in constrained search with A*. We show with extensive experiments on both realistic and randomised graphs how bucket-based queues without tie-breaking can effectively improve the algorithmic performance of exhaustive bi-criteria searches.

Bi-objective Search with Bi-directional A*

Bi-objective search is a well-known algorithmic problem, concerned with finding a set of optimal solutions in a two-dimensional domain. This problem has a wide variety of applications such as planning in transport systems or optimal control in energy systems. Recently, bi-objective A*-based search (BOA*) has shown state-of-the-art performance in large networks. This paper develops a bi-directional variant of BOA*, enriched with several speed-up heuristics. Our experimental results on 1,000 benchmark cases show that our bi-directional A* algorithm for bi-objective search (BOBA*) can optimally solve all of the benchmark cases within the time limit, outperforming the state of the art BOA*, bi-objective Dijkstra and bi-directional bi-objective Dijkstra by an average runtime improvement of a factor of five over all of the benchmark instances.

Versatile and Robust Transient Stability Assessment via Instance Transfer Learning

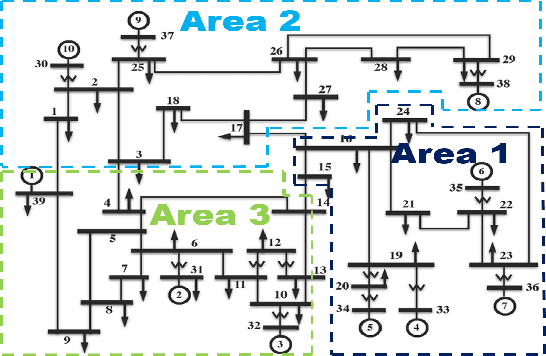
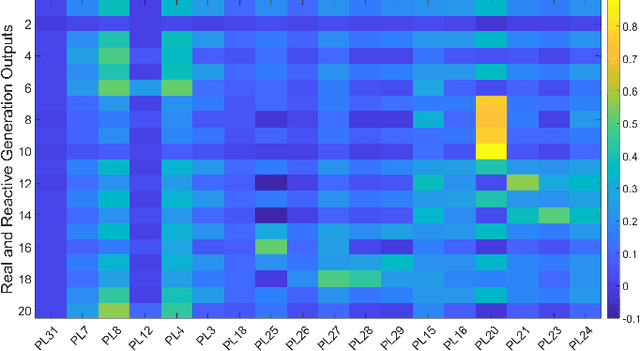
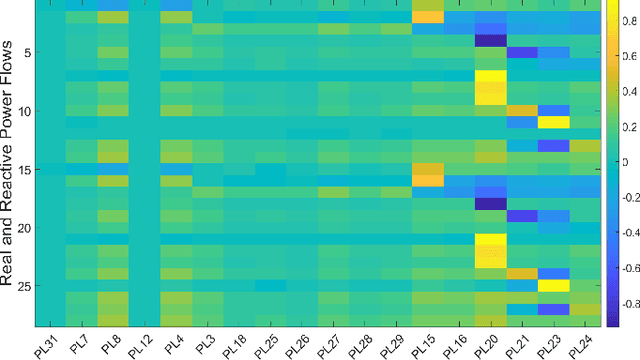
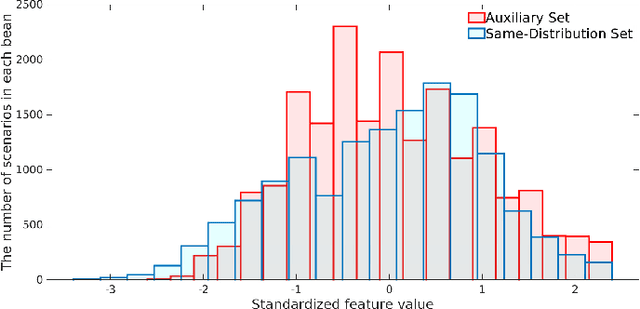
To support N-1 pre-fault transient stability assessment, this paper introduces a new data collection method in a data-driven algorithm incorporating the knowledge of power system dynamics. The domain knowledge on how the disturbance effect will propagate from the fault location to the rest of the network is leveraged to recognise the dominant conditions that determine the stability of a system. Accordingly, we introduce a new concept called Fault-Affected Area, which provides crucial information regarding the unstable region of operation. This information is embedded in an augmented dataset to train an ensemble model using an instance transfer learning framework. The test results on the IEEE 39-bus system verify that this model can accurately predict the stability of previously unseen operational scenarios while reducing the risk of false prediction of unstable instances compared to standard approaches.

Solution Dominance over Constraint Satisfaction Problems

Constraint Satisfaction Problems (CSPs) typically have many solutions that satisfy all constraints. Often though, some solutions are preferred over others, that is, some solutions dominate other solutions. We present solution dominance as a formal framework to reason about such settings. We define Constraint Dominance Problems (CDPs) as CSPs with a dominance relation, that is, a preorder over the solutions of the CSP. This framework captures many well-known variants of constraint satisfaction, including optimization, multi-objective optimization, Max-CSP, minimal models, minimum correction subsets as well as optimization over CP-nets and arbitrary dominance relations. We extend MiniZinc, a declarative language for modeling CSPs, to CDPs by introducing dominance nogoods; these can be derived from dominance relations in a principled way. A generic method for solving arbitrary CDPs incrementally calls a CSP solver and is compatible with any existing solver that supports MiniZinc. This encourages experimenting with different solution dominance relations for a problem, as well as comparing different solvers without having to modify their implementations.

Search Combinators

The ability to model search in a constraint solver can be an essential asset for solving combinatorial problems. However, existing infrastructure for defining search heuristics is often inadequate. Either modeling capabilities are extremely limited or users are faced with a general-purpose programming language whose features are not tailored towards writing search heuristics. As a result, major improvements in performance may remain unexplored. This article introduces search combinators, a lightweight and solver-independent method that bridges the gap between a conceptually simple modeling language for search (high-level, functional and naturally compositional) and an efficient implementation (low-level, imperative and highly non-modular). By allowing the user to define application-tailored search strategies from a small set of primitives, search combinators effectively provide a rich domain-specific language (DSL) for modeling search to the user. Remarkably, this DSL comes at a low implementation cost to the developer of a constraint solver. The article discusses two modular implementation approaches and shows, by empirical evaluation, that search combinators can be implemented without overhead compared to a native, direct implementation in a constraint solver.

View-based Propagator Derivation

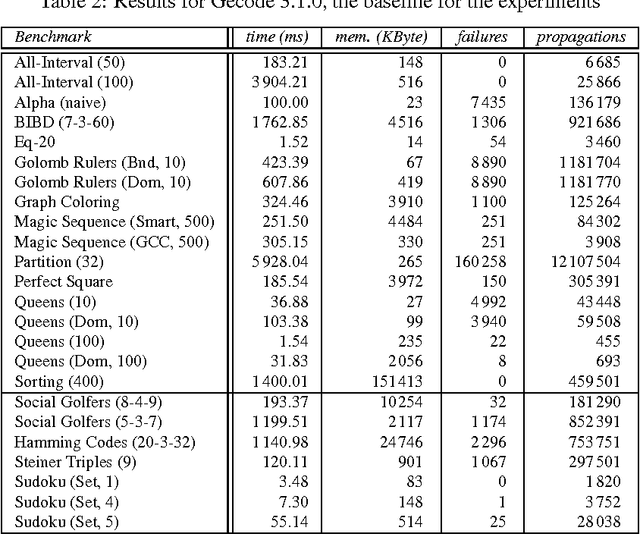
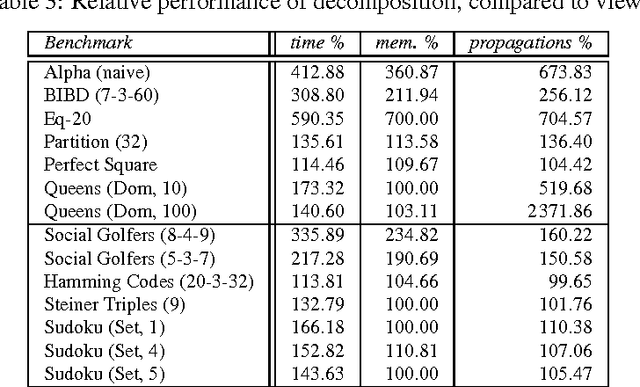
When implementing a propagator for a constraint, one must decide about variants: When implementing min, should one also implement max? Should one implement linear constraints both with unit and non-unit coefficients? Constraint variants are ubiquitous: implementing them requires considerable (if not prohibitive) effort and decreases maintainability, but will deliver better performance than resorting to constraint decomposition. This paper shows how to use views to derive perfect propagator variants. A model for views and derived propagators is introduced. Derived propagators are proved to be indeed perfect in that they inherit essential properties such as correctness and domain and bounds consistency. Techniques for systematically deriving propagators such as transformation, generalization, specialization, and type conversion are developed. The paper introduces an implementation architecture for views that is independent of the underlying constraint programming system. A detailed evaluation of views implemented in Gecode shows that derived propagators are efficient and that views often incur no overhead. Without views, Gecode would either require 180 000 rather than 40 000 lines of propagator code, or would lack many efficient propagator variants. Compared to 8 000 lines of code for views, the reduction in code for propagators yields a 1750% return on investment.

Decomposition During Search for Propagation-Based Constraint Solvers

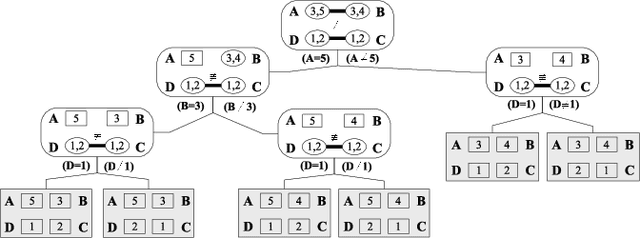
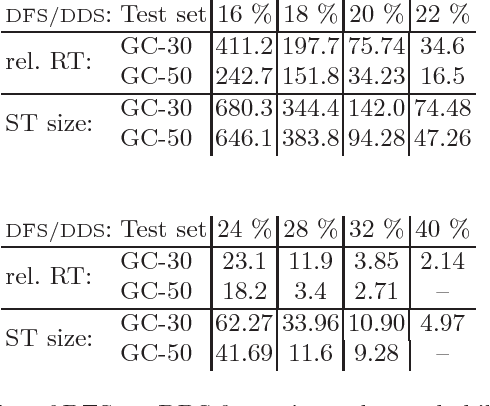
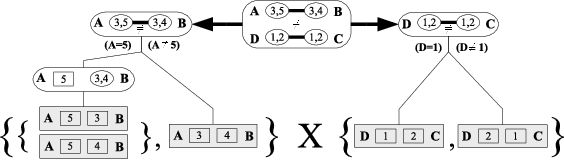
We describe decomposition during search (DDS), an integration of And/Or tree search into propagation-based constraint solvers. The presented search algorithm dynamically decomposes sub-problems of a constraint satisfaction problem into independent partial problems, avoiding redundant work. The paper discusses how DDS interacts with key features that make propagation-based solvers successful: constraint propagation, especially for global constraints, and dynamic search heuristics. We have implemented DDS for the Gecode constraint programming library. Two applications, solution counting in graph coloring and protein structure prediction, exemplify the benefits of DDS in practice.

Perfect Derived Propagators

When implementing a propagator for a constraint, one must decide about variants: When implementing min, should one also implement max? Should one implement linear equations both with and without coefficients? Constraint variants are ubiquitous: implementing them requires considerable (if not prohibitive) effort and decreases maintainability, but will deliver better performance. This paper shows how to use variable views, previously introduced for an implementation architecture, to derive perfect propagator variants. A model for views and derived propagators is introduced. Derived propagators are proved to be indeed perfect in that they inherit essential properties such as correctness and domain and bounds consistency. Techniques for systematically deriving propagators such as transformation, generalization, specialization, and channeling are developed for several variable domains. We evaluate the massive impact of derived propagators. Without derived propagators, Gecode would require 140000 rather than 40000 lines of code for propagators.