View-based Propagator Derivation

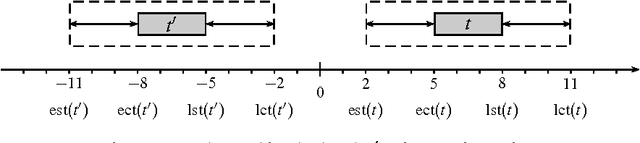
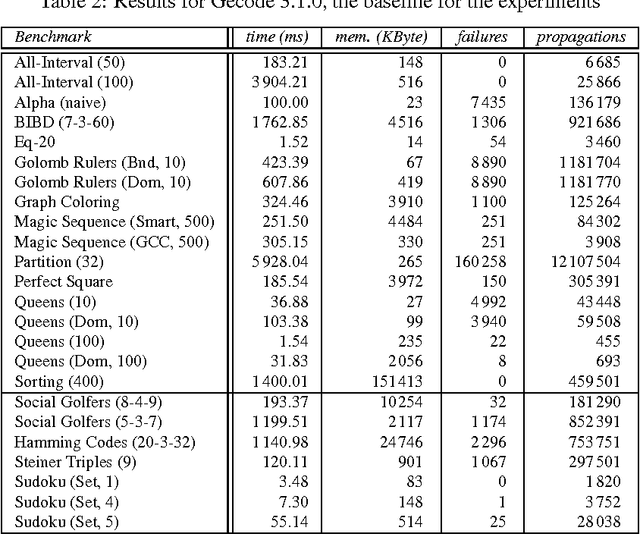
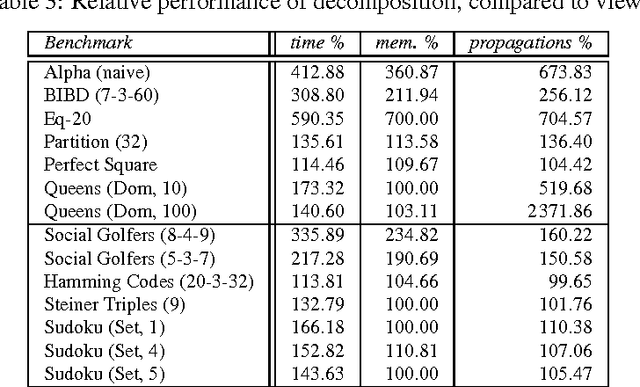
When implementing a propagator for a constraint, one must decide about variants: When implementing min, should one also implement max? Should one implement linear constraints both with unit and non-unit coefficients? Constraint variants are ubiquitous: implementing them requires considerable (if not prohibitive) effort and decreases maintainability, but will deliver better performance than resorting to constraint decomposition. This paper shows how to use views to derive perfect propagator variants. A model for views and derived propagators is introduced. Derived propagators are proved to be indeed perfect in that they inherit essential properties such as correctness and domain and bounds consistency. Techniques for systematically deriving propagators such as transformation, generalization, specialization, and type conversion are developed. The paper introduces an implementation architecture for views that is independent of the underlying constraint programming system. A detailed evaluation of views implemented in Gecode shows that derived propagators are efficient and that views often incur no overhead. Without views, Gecode would either require 180 000 rather than 40 000 lines of propagator code, or would lack many efficient propagator variants. Compared to 8 000 lines of code for views, the reduction in code for propagators yields a 1750% return on investment.