View-based Propagator Derivation

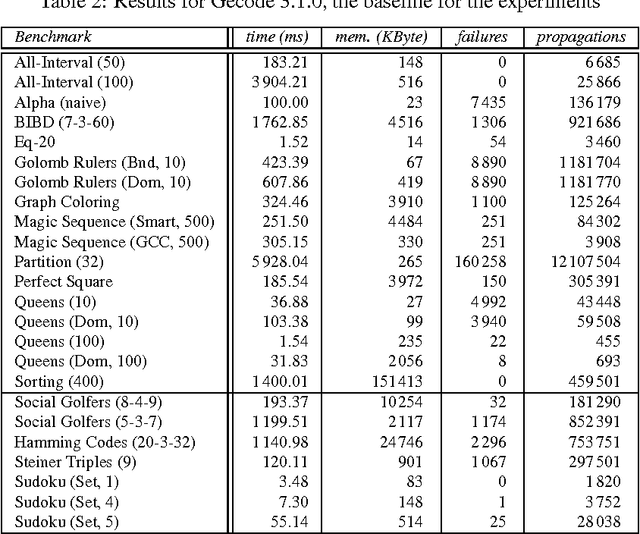
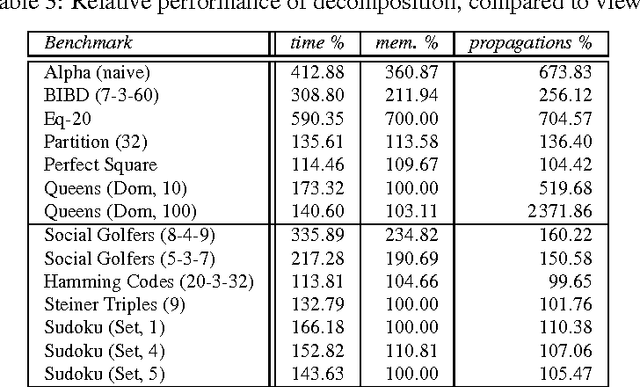
When implementing a propagator for a constraint, one must decide about variants: When implementing min, should one also implement max? Should one implement linear constraints both with unit and non-unit coefficients? Constraint variants are ubiquitous: implementing them requires considerable (if not prohibitive) effort and decreases maintainability, but will deliver better performance than resorting to constraint decomposition. This paper shows how to use views to derive perfect propagator variants. A model for views and derived propagators is introduced. Derived propagators are proved to be indeed perfect in that they inherit essential properties such as correctness and domain and bounds consistency. Techniques for systematically deriving propagators such as transformation, generalization, specialization, and type conversion are developed. The paper introduces an implementation architecture for views that is independent of the underlying constraint programming system. A detailed evaluation of views implemented in Gecode shows that derived propagators are efficient and that views often incur no overhead. Without views, Gecode would either require 180 000 rather than 40 000 lines of propagator code, or would lack many efficient propagator variants. Compared to 8 000 lines of code for views, the reduction in code for propagators yields a 1750% return on investment.

Perfect Derived Propagators

When implementing a propagator for a constraint, one must decide about variants: When implementing min, should one also implement max? Should one implement linear equations both with and without coefficients? Constraint variants are ubiquitous: implementing them requires considerable (if not prohibitive) effort and decreases maintainability, but will deliver better performance. This paper shows how to use variable views, previously introduced for an implementation architecture, to derive perfect propagator variants. A model for views and derived propagators is introduced. Derived propagators are proved to be indeed perfect in that they inherit essential properties such as correctness and domain and bounds consistency. Techniques for systematically deriving propagators such as transformation, generalization, specialization, and channeling are developed for several variable domains. We evaluate the massive impact of derived propagators. Without derived propagators, Gecode would require 140000 rather than 40000 lines of code for propagators.

Efficient constraint propagation engines

This paper presents a model and implementation techniques for speeding up constraint propagation. Three fundamental approaches to improving constraint propagation based on propagators as implementations of constraints are explored: keeping track of which propagators are at fixpoint, choosing which propagator to apply next, and how to combine several propagators for the same constraint. We show how idempotence reasoning and events help track fixpoints more accurately. We improve these methods by using them dynamically (taking into account current domains to improve accuracy). We define priority-based approaches to choosing a next propagator and show that dynamic priorities can improve propagation. We illustrate that the use of multiple propagators for the same constraint can be advantageous with priorities, and introduce staged propagators that combine the effects of multiple propagators with priorities for greater efficiency.