New random projections for isotropic kernels using stable spectral distributions

Rahimi and Recht [31] introduced the idea of decomposing shift-invariant kernels by randomly sampling from their spectral distribution. This famous technique, known as Random Fourier Features (RFF), is in principle applicable to any shift-invariant kernel whose spectral distribution can be identified and simulated. In practice, however, it is usually applied to the Gaussian kernel because of its simplicity, since its spectral distribution is also Gaussian. Clearly, simple spectral sampling formulas would be desirable for broader classes of kernel functions. In this paper, we propose to decompose spectral kernel distributions as a scale mixture of $\alpha$-stable random vectors. This provides a simple and ready-to-use spectral sampling formula for a very large class of multivariate shift-invariant kernels, including exponential power kernels, generalized Mat\'ern kernels, generalized Cauchy kernels, as well as newly introduced kernels such as the Beta, Kummer, and Tricomi kernels. In particular, we show that the spectral densities of all these kernels are scale mixtures of the multivariate Gaussian distribution. This provides a very simple way to modify existing Random Fourier Features software based on Gaussian kernels to cover a much richer class of multivariate kernels. This result has broad applications for support vector machines, kernel ridge regression, Gaussian processes, and other kernel-based machine learning techniques for which the random Fourier features technique is applicable.

Studying the Performance of the Jellyfish Search Optimiser for the Application of Projection Pursuit

The projection pursuit (PP) guided tour interactively optimises a criteria function known as the PP index, to explore high-dimensional data by revealing interesting projections. The optimisation in PP can be non-trivial, involving non-smooth functions and optima with a small squint angle, detectable only from close proximity. To address these challenges, this study investigates the performance of a recently introduced swarm-based algorithm, Jellyfish Search Optimiser (JSO), for optimising PP indexes. The performance of JSO for visualising data is evaluated across various hyper-parameter settings and compared with existing optimisers. Additionally, this work proposes novel methods to quantify two properties of the PP index, smoothness and squintability that capture the complexities inherent in PP optimisation problems. These two metrics are evaluated along with JSO hyper-parameters to determine their effects on JSO success rate. Our numerical results confirm the positive impact of these metrics on the JSO success rate, with squintability being the most significant. The JSO algorithm has been implemented in the tourr package and functions to calculate smoothness and squintability are available in the ferrn package.

From attention to profit: quantitative trading strategy based on transformer

In traditional quantitative trading practice, navigating the complicated and dynamic financial market presents a persistent challenge. Former machine learning approaches have struggled to fully capture various market variables, often ignore long-term information and fail to catch up with essential signals that may lead the profit. This paper introduces an enhanced transformer architecture and designs a novel factor based on the model. By transfer learning from sentiment analysis, the proposed model not only exploits its original inherent advantages in capturing long-range dependencies and modelling complex data relationships but is also able to solve tasks with numerical inputs and accurately forecast future returns over a period. This work collects more than 5,000,000 rolling data of 4,601 stocks in the Chinese capital market from 2010 to 2019. The results of this study demonstrated the model's superior performance in predicting stock trends compared with other 100 factor-based quantitative strategies with lower turnover rates and a more robust half-life period. Notably, the model's innovative use transformer to establish factors, in conjunction with market sentiment information, has been shown to enhance the accuracy of trading signals significantly, thereby offering promising implications for the future of quantitative trading strategies.

Unleashing the potential of prompt engineering in Large Language Models: a comprehensive review

This paper delves into the pivotal role of prompt engineering in unleashing the capabilities of Large Language Models (LLMs). Prompt engineering is the process of structuring input text for LLMs and is a technique integral to optimizing the efficacy of LLMs. This survey elucidates foundational principles of prompt engineering, such as role-prompting, one-shot, and few-shot prompting, as well as more advanced methodologies such as the chain-of-thought and tree-of-thoughts prompting. The paper sheds light on how external assistance in the form of plugins can assist in this task, and reduce machine hallucination by retrieving external knowledge. We subsequently delineate prospective directions in prompt engineering research, emphasizing the need for a deeper understanding of structures and the role of agents in Artificial Intelligence-Generated Content (AIGC) tools. We discuss how to assess the efficacy of prompt methods from different perspectives and using different methods. Finally, we gather information about the application of prompt engineering in such fields as education and programming, showing its transformative potential. This comprehensive survey aims to serve as a friendly guide for anyone venturing through the big world of LLMs and prompt engineering.

Simultaneous upper and lower bounds of American option prices with hedging via neural networks

In this paper, we introduce two methods to solve the American-style option pricing problem and its dual form at the same time using neural networks. Without applying nested Monte Carlo, the first method uses a series of neural networks to simultaneously compute both the lower and upper bounds of the option price, and the second one accomplishes the same goal with one global network. The avoidance of extra simulations and the use of neural networks significantly reduce the computational complexity and allow us to price Bermudan options with frequent exercise opportunities in high dimensions, as illustrated by the provided numerical experiments. As a by-product, these methods also derive a hedging strategy for the option, which can also be used as a control variate for variance reduction.

Versatile and Robust Transient Stability Assessment via Instance Transfer Learning

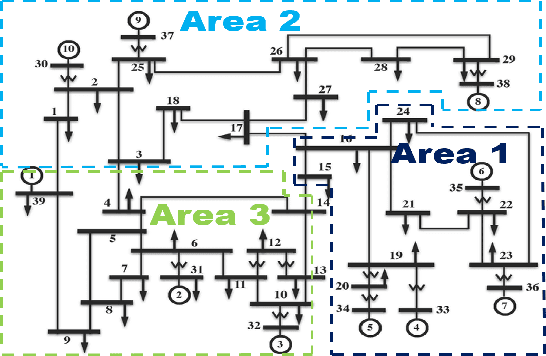
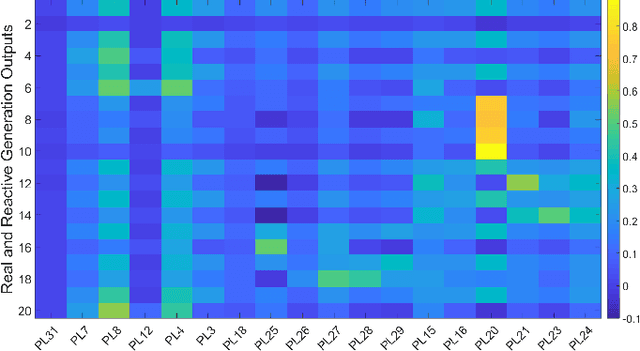
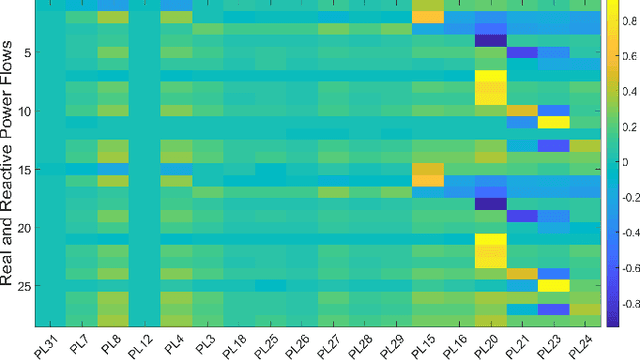
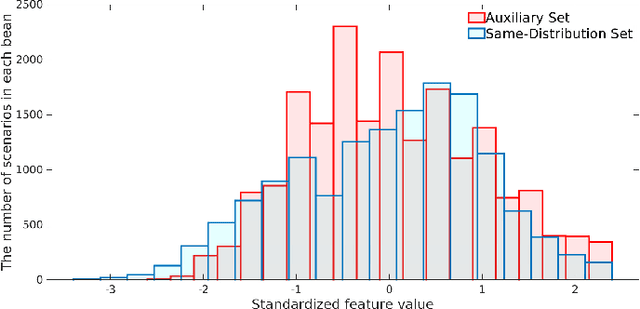
To support N-1 pre-fault transient stability assessment, this paper introduces a new data collection method in a data-driven algorithm incorporating the knowledge of power system dynamics. The domain knowledge on how the disturbance effect will propagate from the fault location to the rest of the network is leveraged to recognise the dominant conditions that determine the stability of a system. Accordingly, we introduce a new concept called Fault-Affected Area, which provides crucial information regarding the unstable region of operation. This information is embedded in an augmented dataset to train an ensemble model using an instance transfer learning framework. The test results on the IEEE 39-bus system verify that this model can accurately predict the stability of previously unseen operational scenarios while reducing the risk of false prediction of unstable instances compared to standard approaches.

Deep neural network for optimal retirement consumption in defined contribution pension system

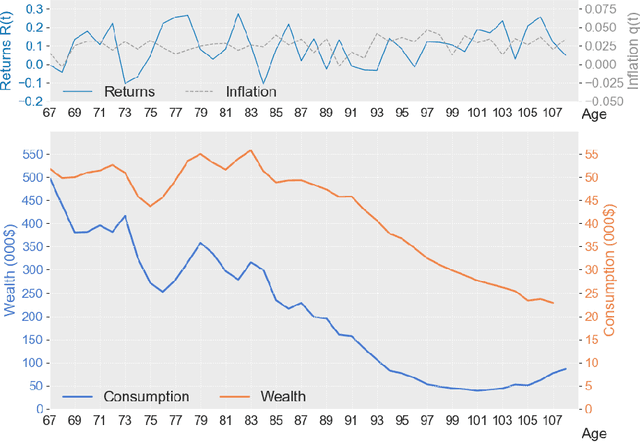
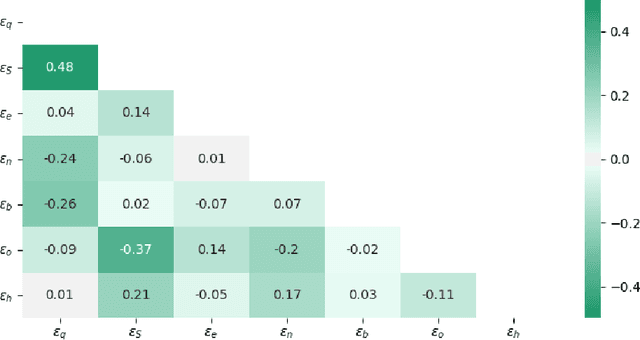
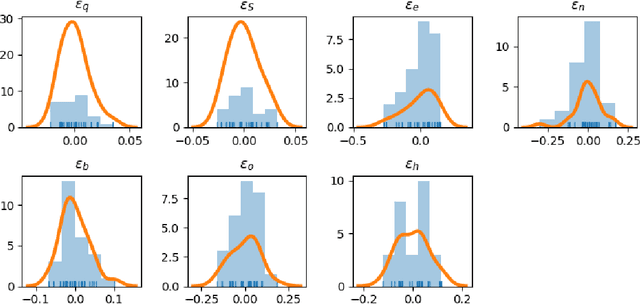
In this paper, we develop a deep neural network approach to solve a lifetime expected mortality-weighted utility-based model for optimal consumption in the decumulation phase of a defined contribution pension system. We formulate this problem as a multi-period finite-horizon stochastic control problem and train a deep neural network policy representing consumption decisions. The optimal consumption policy is determined by personal information about the retiree such as age, wealth, risk aversion and bequest motive, as well as a series of economic and financial variables including inflation rates and asset returns jointly simulated from a proposed seven-factor economic scenario generator calibrated from market data. We use the Australian pension system as an example, with consideration of the government-funded means-tested Age Pension and other practical aspects such as fund management fees. The key findings from our numerical tests are as follows. First, our deep neural network optimal consumption policy, which adapts to changes in market conditions, outperforms deterministic drawdown rules proposed in the literature. Moreover, the out-of-sample outperformance ratios increase as the number of training iterations increases, eventually reaching outperformance on all testing scenarios after less than 10 minutes of training. Second, a sensitivity analysis is performed to reveal how risk aversion and bequest motives change the consumption over a retiree's lifetime under this utility framework. Third, we provide the optimal consumption rate with different starting wealth balances. We observe that optimal consumption rates are not proportional to initial wealth due to the Age Pension payment. Forth, with the same initial wealth balance and utility parameter settings, the optimal consumption level is different between males and females due to gender differences in mortality.

Deep neural networks algorithms for stochastic control problems on finite horizon, Part 2: numerical applications

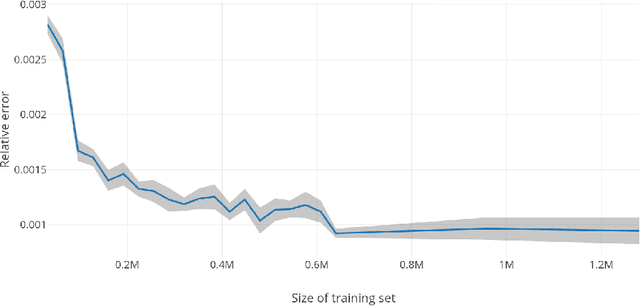
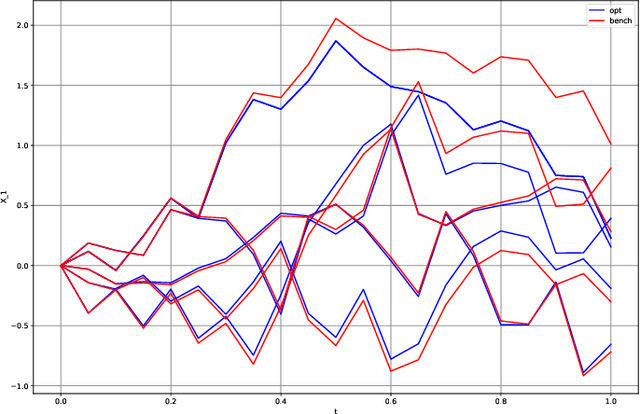
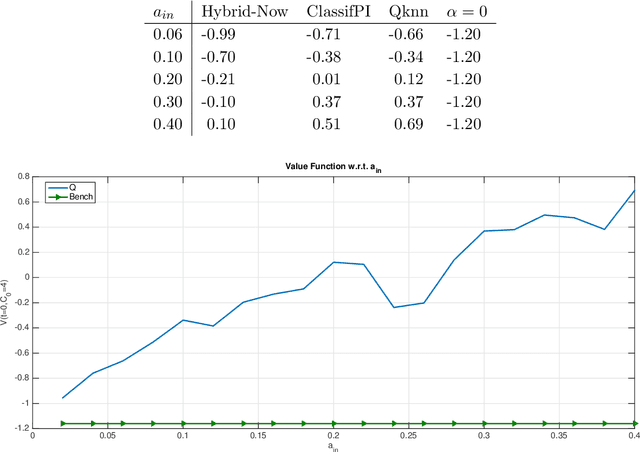
This paper presents several numerical applications of deep learning-based algorithms that have been analyzed in [11]. Numerical and comparative tests using TensorFlow illustrate the performance of our different algorithms, namely control learning by performance iteration (algorithms NNcontPI and ClassifPI), control learning by hybrid iteration (algorithms Hybrid-Now and Hybrid-LaterQ), on the 100-dimensional nonlinear PDEs examples from [6] and on quadratic Backward Stochastic Differential equations as in [5]. We also provide numerical results for an option hedging problem in finance, and energy storage problems arising in the valuation of gas storage and in microgrid management.

Deep neural networks algorithms for stochastic control problems on finite horizon, part I: convergence analysis

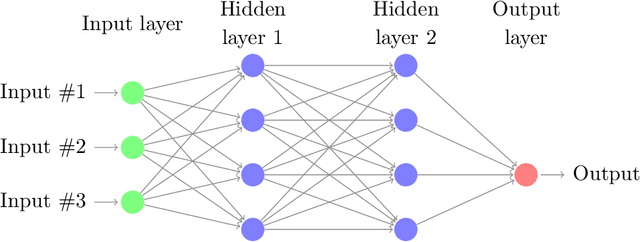
This paper develops algorithms for high-dimensional stochastic control problems based on deep learning and dynamic programming (DP). Differently from the classical approximate DP approach, we first approximate the optimal policy by means of neural networks in the spirit of deep reinforcement learning, and then the value function by Monte Carlo regression. This is achieved in the DP recursion by performance or hybrid iteration, and regress now or later/quantization methods from numerical probabilities. We provide a theoretical justification of these algorithms. Consistency and rate of convergence for the control and value function estimates are analyzed and expressed in terms of the universal approximation error of the neural networks. Numerical results on various applications are presented in a companion paper [2] and illustrate the performance of our algorithms.