LightSBB-M: Bridging Schrödinger and Bass for Generative Diffusion Modeling

The Schrodinger Bridge and Bass (SBB) formulation, which jointly controls drift and volatility, is an established extension of the classical Schrodinger Bridge (SB). Building on this framework, we introduce LightSBB-M, an algorithm that computes the optimal SBB transport plan in only a few iterations. The method exploits a dual representation of the SBB objective to obtain analytic expressions for the optimal drift and volatility, and it incorporates a tunable parameter beta greater than zero that interpolates between pure drift (the Schrodinger Bridge) and pure volatility (Bass martingale transport). We show that LightSBB-M achieves the lowest 2-Wasserstein distance on synthetic datasets against state-of-the-art SB and diffusion baselines with up to 32 percent improvement. We also illustrate the generative capability of the framework on an unpaired image-to-image translation task (adult to child faces in FFHQ). These findings demonstrate that LightSBB-M provides a scalable, high-fidelity SBB solver that outperforms existing SB and diffusion baselines across both synthetic and real-world generative tasks. The code is available at https://github.com/alexouadi/LightSBB-M.

Model-free policy gradient for discrete-time mean-field control

We study model-free policy learning for discrete-time mean-field control (MFC) problems with finite state space and compact action space. In contrast to the extensive literature on value-based methods for MFC, policy-based approaches remain largely unexplored due to the intrinsic dependence of transition kernels and rewards on the evolving population state distribution, which prevents the direct use of likelihood-ratio estimators of policy gradients from classical single-agent reinforcement learning. We introduce a novel perturbation scheme on the state-distribution flow and prove that the gradient of the resulting perturbed value function converges to the true policy gradient as the perturbation magnitude vanishes. This construction yields a fully model-free estimator based solely on simulated trajectories and an auxiliary estimate of the sensitivity of the state distribution. Building on this framework, we develop MF-REINFORCE, a model-free policy gradient algorithm for MFC, and establish explicit quantitative bounds on its bias and mean-squared error. Numerical experiments on representative mean-field control tasks demonstrate the effectiveness of the proposed approach.

Robust time series generation via Schrödinger Bridge: a comprehensive evaluation

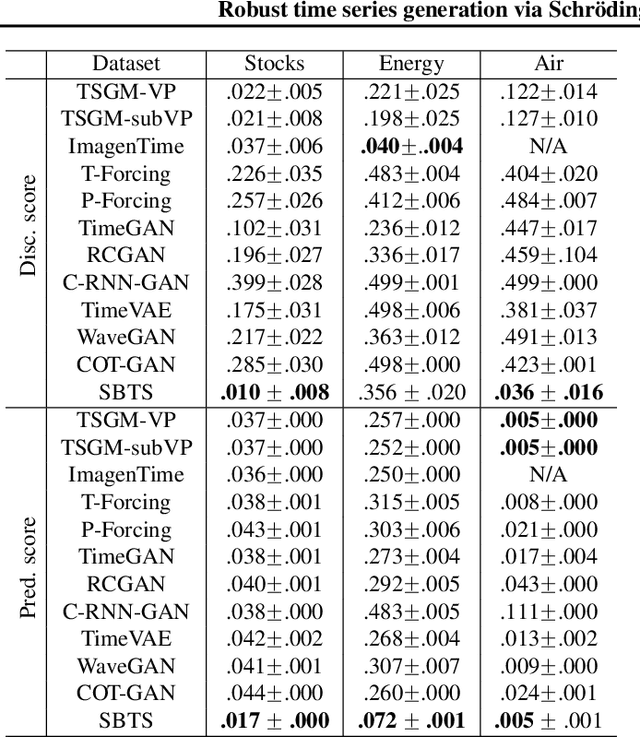
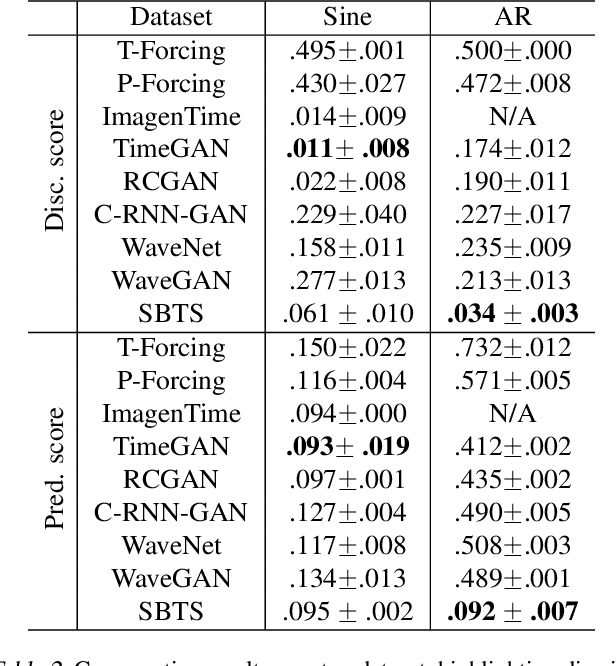
We investigate the generative capabilities of the Schr\"odinger Bridge (SB) approach for time series. The SB framework formulates time series synthesis as an entropic optimal interpolation transport problem between a reference probability measure on path space and a target joint distribution. This results in a stochastic differential equation over a finite horizon that accurately captures the temporal dynamics of the target time series. While the SB approach has been largely explored in fields like image generation, there is a scarcity of studies for its application to time series. In this work, we bridge this gap by conducting a comprehensive evaluation of the SB method's robustness and generative performance. We benchmark it against state-of-the-art (SOTA) time series generation methods across diverse datasets, assessing its strengths, limitations, and capacity to model complex temporal dependencies. Our results offer valuable insights into the SB framework's potential as a versatile and robust tool for time series generation.

Full error analysis of policy gradient learning algorithms for exploratory linear quadratic mean-field control problem in continuous time with common noise

We consider reinforcement learning (RL) methods for finding optimal policies in linear quadratic (LQ) mean field control (MFC) problems over an infinite horizon in continuous time, with common noise and entropy regularization. We study policy gradient (PG) learning and first demonstrate convergence in a model-based setting by establishing a suitable gradient domination condition.Next, our main contribution is a comprehensive error analysis, where we prove the global linear convergence and sample complexity of the PG algorithm with two-point gradient estimates in a model-free setting with unknown parameters. In this setting, the parameterized optimal policies are learned from samples of the states and population distribution.Finally, we provide numerical evidence supporting the convergence of our implemented algorithms.

Control randomisation approach for policy gradient and application to reinforcement learning in optimal switching

We propose a comprehensive framework for policy gradient methods tailored to continuous time reinforcement learning. This is based on the connection between stochastic control problems and randomised problems, enabling applications across various classes of Markovian continuous time control problems, beyond diffusion models, including e.g. regular, impulse and optimal stopping/switching problems. By utilizing change of measure in the control randomisation technique, we derive a new policy gradient representation for these randomised problems, featuring parametrised intensity policies. We further develop actor-critic algorithms specifically designed to address general Markovian stochastic control issues. Our framework is demonstrated through its application to optimal switching problems, with two numerical case studies in the energy sector focusing on real options.

Actor critic learning algorithms for mean-field control with moment neural networks

We develop a new policy gradient and actor-critic algorithm for solving mean-field control problems within a continuous time reinforcement learning setting. Our approach leverages a gradient-based representation of the value function, employing parametrized randomized policies. The learning for both the actor (policy) and critic (value function) is facilitated by a class of moment neural network functions on the Wasserstein space of probability measures, and the key feature is to sample directly trajectories of distributions. A central challenge addressed in this study pertains to the computational treatment of an operator specific to the mean-field framework. To illustrate the effectiveness of our methods, we provide a comprehensive set of numerical results. These encompass diverse examples, including multi-dimensional settings and nonlinear quadratic mean-field control problems with controlled volatility.

Generative modeling for time series via Schr{ö}dinger bridge

We propose a novel generative model for time series based on Schr{\"o}dinger bridge (SB) approach. This consists in the entropic interpolation via optimal transport between a reference probability measure on path space and a target measure consistent with the joint data distribution of the time series. The solution is characterized by a stochastic differential equation on finite horizon with a path-dependent drift function, hence respecting the temporal dynamics of the time series distribution. We can estimate the drift function from data samples either by kernel regression methods or with LSTM neural networks, and the simulation of the SB diffusion yields new synthetic data samples of the time series. The performance of our generative model is evaluated through a series of numerical experiments. First, we test with a toy autoregressive model, a GARCH Model, and the example of fractional Brownian motion, and measure the accuracy of our algorithm with marginal and temporal dependencies metrics. Next, we use our SB generated synthetic samples for the application to deep hedging on real-data sets. Finally, we illustrate the SB approach for generating sequence of images.

Actor-Critic learning for mean-field control in continuous time

We study policy gradient for mean-field control in continuous time in a reinforcement learning setting. By considering randomised policies with entropy regularisation, we derive a gradient expectation representation of the value function, which is amenable to actor-critic type algorithms, where the value functions and the policies are learnt alternately based on observation samples of the state and model-free estimation of the population state distribution, either by offline or online learning. In the linear-quadratic mean-field framework, we obtain an exact parametrisation of the actor and critic functions defined on the Wasserstein space. Finally, we illustrate the results of our algorithms with some numerical experiments on concrete examples.

Mean-field neural networks-based algorithms for McKean-Vlasov control problems *

This paper is devoted to the numerical resolution of McKean-Vlasov control problems via the class of mean-field neural networks introduced in our companion paper [25] in order to learn the solution on the Wasserstein space. We propose several algorithms either based on dynamic programming with control learning by policy or value iteration, or backward SDE from stochastic maximum principle with global or local loss functions. Extensive numerical results on different examples are presented to illustrate the accuracy of each of our eight algorithms. We discuss and compare the pros and cons of all the tested methods.

Mean-field neural networks: learning mappings on Wasserstein space

We study the machine learning task for models with operators mapping between the Wasserstein space of probability measures and a space of functions, like e.g. in mean-field games/control problems. Two classes of neural networks, based on bin density and on cylindrical approximation, are proposed to learn these so-called mean-field functions, and are theoretically supported by universal approximation theorems. We perform several numerical experiments for training these two mean-field neural networks, and show their accuracy and efficiency in the generalization error with various test distributions. Finally, we present different algorithms relying on mean-field neural networks for solving time-dependent mean-field problems, and illustrate our results with numerical tests for the example of a semi-linear partial differential equation in the Wasserstein space of probability measures.