Neural networks-based backward scheme for fully nonlinear PDEs

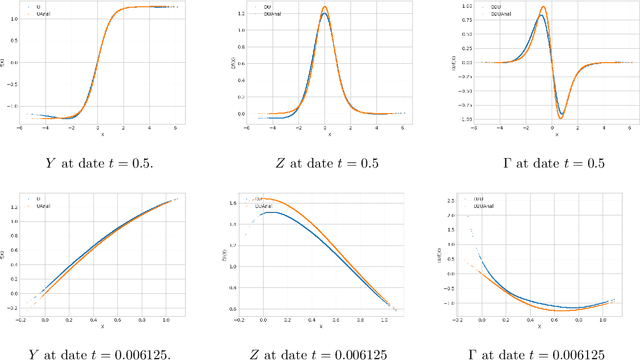
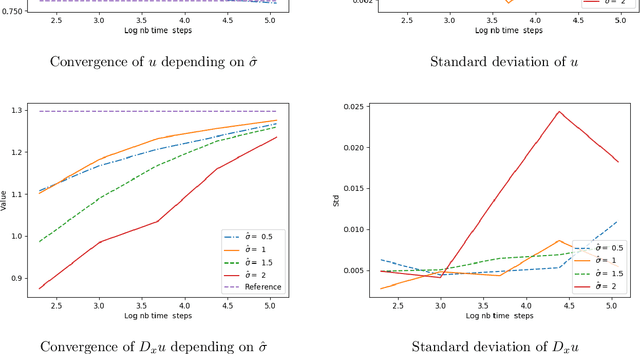
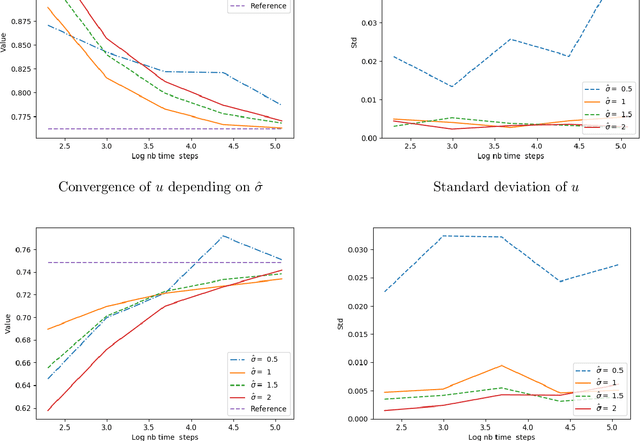
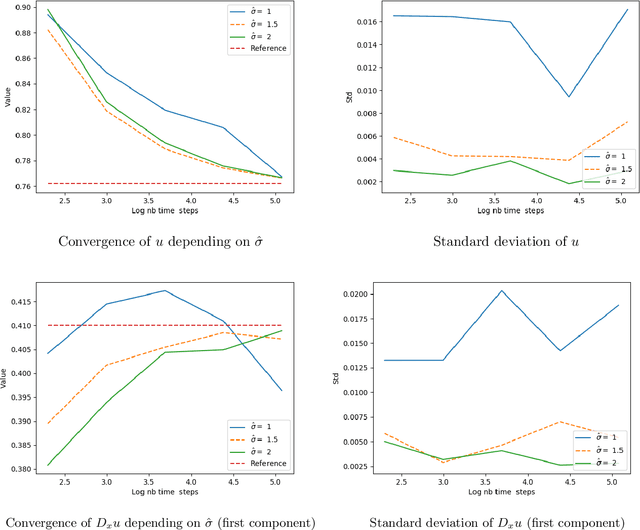
We propose a numerical method for solving high dimensional fully nonlinear partial differential equations (PDEs). Our algorithm estimates simultaneously by backward time induction the solution and its gradient by multi-layer neural networks, through a sequence of learning problems obtained from the minimization of suitable quadratic loss functions and training simulations. This methodology extends to the fully non-linear case the approach recently proposed in [HPW19] for semi-linear PDEs. Numerical tests illustrate the performance and accuracy of our method on several examples in high dimension with nonlinearity on the Hessian term including a linear quadratic control problem with control on the diffusion coefficient.

Deep neural networks algorithms for stochastic control problems on finite horizon, Part 2: numerical applications

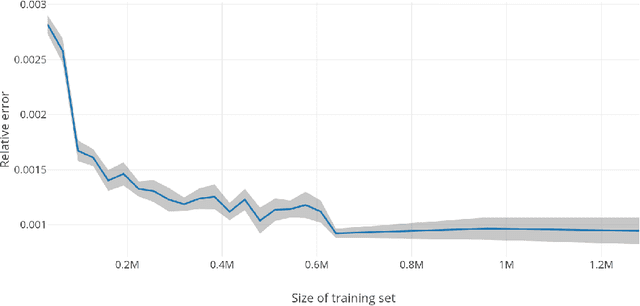
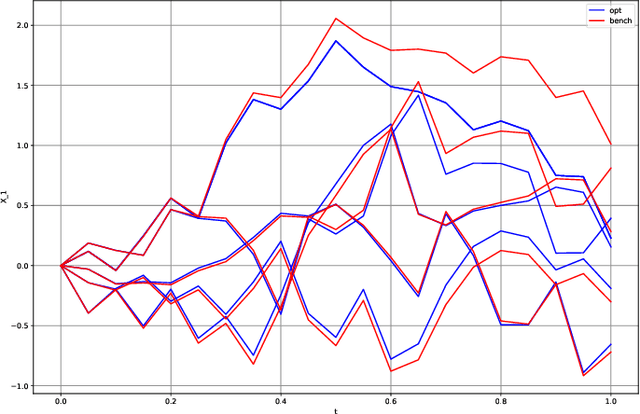
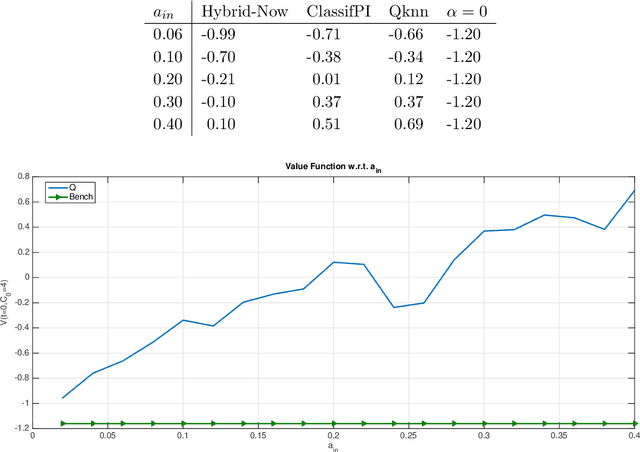
This paper presents several numerical applications of deep learning-based algorithms that have been analyzed in [11]. Numerical and comparative tests using TensorFlow illustrate the performance of our different algorithms, namely control learning by performance iteration (algorithms NNcontPI and ClassifPI), control learning by hybrid iteration (algorithms Hybrid-Now and Hybrid-LaterQ), on the 100-dimensional nonlinear PDEs examples from [6] and on quadratic Backward Stochastic Differential equations as in [5]. We also provide numerical results for an option hedging problem in finance, and energy storage problems arising in the valuation of gas storage and in microgrid management.