LightSBB-M: Bridging Schrödinger and Bass for Generative Diffusion Modeling

The Schrodinger Bridge and Bass (SBB) formulation, which jointly controls drift and volatility, is an established extension of the classical Schrodinger Bridge (SB). Building on this framework, we introduce LightSBB-M, an algorithm that computes the optimal SBB transport plan in only a few iterations. The method exploits a dual representation of the SBB objective to obtain analytic expressions for the optimal drift and volatility, and it incorporates a tunable parameter beta greater than zero that interpolates between pure drift (the Schrodinger Bridge) and pure volatility (Bass martingale transport). We show that LightSBB-M achieves the lowest 2-Wasserstein distance on synthetic datasets against state-of-the-art SB and diffusion baselines with up to 32 percent improvement. We also illustrate the generative capability of the framework on an unpaired image-to-image translation task (adult to child faces in FFHQ). These findings demonstrate that LightSBB-M provides a scalable, high-fidelity SBB solver that outperforms existing SB and diffusion baselines across both synthetic and real-world generative tasks. The code is available at https://github.com/alexouadi/LightSBB-M.

Robust time series generation via Schrödinger Bridge: a comprehensive evaluation

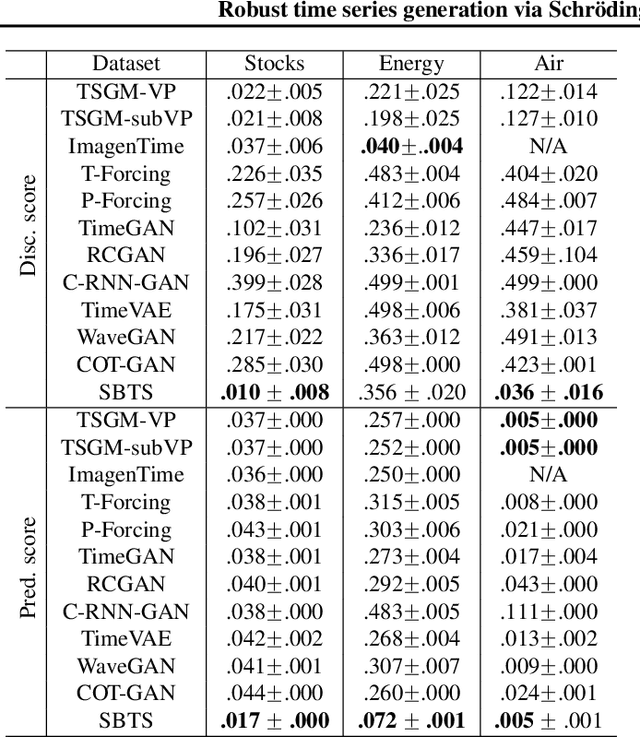
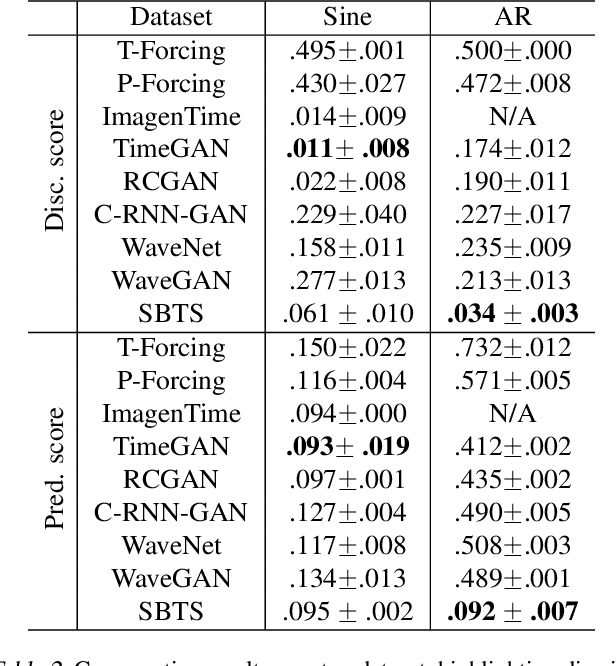
We investigate the generative capabilities of the Schr\"odinger Bridge (SB) approach for time series. The SB framework formulates time series synthesis as an entropic optimal interpolation transport problem between a reference probability measure on path space and a target joint distribution. This results in a stochastic differential equation over a finite horizon that accurately captures the temporal dynamics of the target time series. While the SB approach has been largely explored in fields like image generation, there is a scarcity of studies for its application to time series. In this work, we bridge this gap by conducting a comprehensive evaluation of the SB method's robustness and generative performance. We benchmark it against state-of-the-art (SOTA) time series generation methods across diverse datasets, assessing its strengths, limitations, and capacity to model complex temporal dependencies. Our results offer valuable insights into the SB framework's potential as a versatile and robust tool for time series generation.