Enhanced Methods for the Weight Constrained Shortest Path Problem: Constrained Path Finding Meets Bi-objective Search

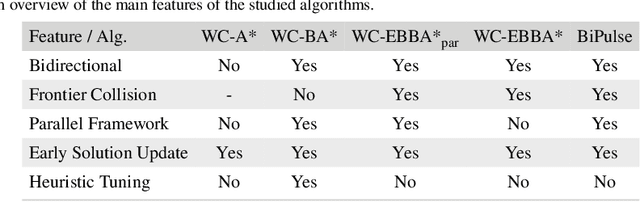
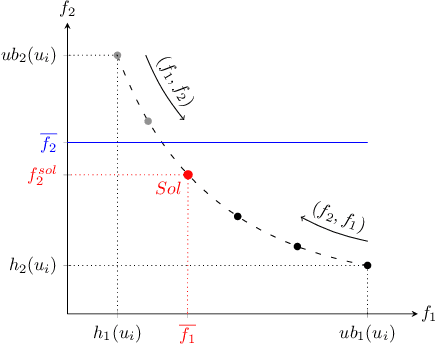
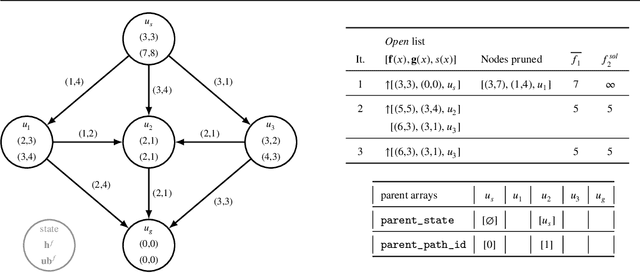
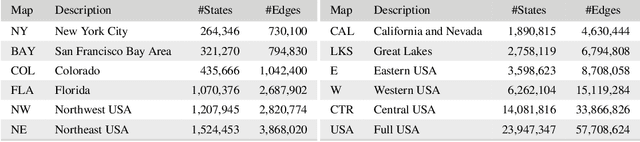
The classic problem of \textit{constrained path finding} is a well-studied but yet challenging topic in AI with a broad range of applications in various areas such communication and transportation. The Weight Constrained Shortest Path Problem (WCSPP), as the base form of constrained path finding with only one side constraint, aims to plan a cost optimum path whose weight/resource usage is limited. Given the bi-criteria nature of the problem (i.e., dealing with cost and weight of paths), methods addressing the WCSPP have some common properties with bi-objective search. This paper leverages the recent state-of-the-art A*-based techniques in both constrained path finding and bi-objective search and presents two exact solution approaches to the WCSPP, both capable of solving hard problem instances on very large graphs. We empirically evaluate the performance of our algorithms on a new set of large and realistic problem instances and show their advantages over the state-of-the-art algorithms in both time and space metrics. This paper also investigates the importance of priority queues in constrained search with A*. We show with extensive experiments on both realistic and randomised graphs how bucket-based queues without tie-breaking can effectively improve the algorithmic performance of exhaustive bi-criteria searches.