Real-Time Energy-Optimal Path Planning for Electric Vehicles

The rapid adoption of electric vehicles (EVs) in modern transport systems has made energy-aware routing a critical task in their successful integration, especially within large-scale networks. In cases where an EV's remaining energy is limited and charging locations are not easily accessible, some destinations may only be reachable through an energy-optimal path: a route that consumes less energy than all other alternatives. The feasibility of such energy-efficient paths depends heavily on the accuracy of the energy model used for planning, and thus failing to account for vehicle dynamics can lead to inaccurate energy estimates, rendering some planned routes infeasible in reality. This paper explores the impact of vehicle dynamics on energy-optimal path planning for EVs. We develop an accurate energy model that incorporates key vehicle dynamics parameters into energy calculations, thereby reducing the risk of planning infeasible paths under battery constraints. The paper also introduces two novel online reweighting functions that allow for a faster, pre-processing free, pathfinding in the presence of negative energy costs resulting from regenerative braking, making them ideal for real-time applications. Through extensive experimentation on real-world transport networks, we demonstrate that our approach considerably enhances energy-optimal pathfinding for EVs in both computational efficiency and energy estimation accuracy.

Enhanced Methods for the Weight Constrained Shortest Path Problem: Constrained Path Finding Meets Bi-objective Search

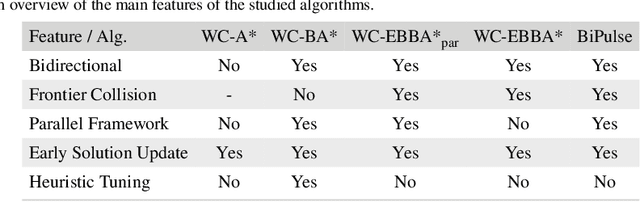
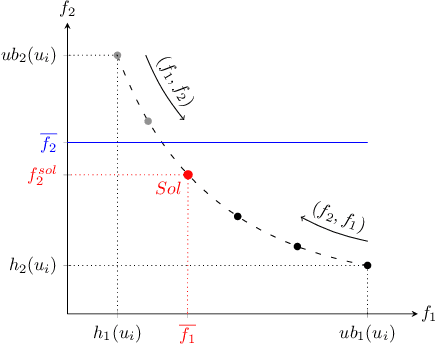
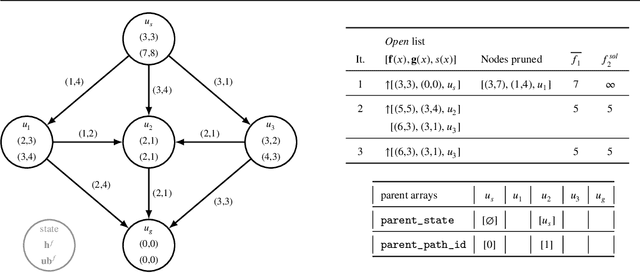
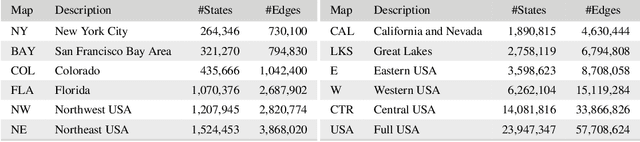
The classic problem of \textit{constrained path finding} is a well-studied but yet challenging topic in AI with a broad range of applications in various areas such communication and transportation. The Weight Constrained Shortest Path Problem (WCSPP), as the base form of constrained path finding with only one side constraint, aims to plan a cost optimum path whose weight/resource usage is limited. Given the bi-criteria nature of the problem (i.e., dealing with cost and weight of paths), methods addressing the WCSPP have some common properties with bi-objective search. This paper leverages the recent state-of-the-art A*-based techniques in both constrained path finding and bi-objective search and presents two exact solution approaches to the WCSPP, both capable of solving hard problem instances on very large graphs. We empirically evaluate the performance of our algorithms on a new set of large and realistic problem instances and show their advantages over the state-of-the-art algorithms in both time and space metrics. This paper also investigates the importance of priority queues in constrained search with A*. We show with extensive experiments on both realistic and randomised graphs how bucket-based queues without tie-breaking can effectively improve the algorithmic performance of exhaustive bi-criteria searches.

Bi-objective Search with Bi-directional A*

Bi-objective search is a well-known algorithmic problem, concerned with finding a set of optimal solutions in a two-dimensional domain. This problem has a wide variety of applications such as planning in transport systems or optimal control in energy systems. Recently, bi-objective A*-based search (BOA*) has shown state-of-the-art performance in large networks. This paper develops a bi-directional variant of BOA*, enriched with several speed-up heuristics. Our experimental results on 1,000 benchmark cases show that our bi-directional A* algorithm for bi-objective search (BOBA*) can optimally solve all of the benchmark cases within the time limit, outperforming the state of the art BOA*, bi-objective Dijkstra and bi-directional bi-objective Dijkstra by an average runtime improvement of a factor of five over all of the benchmark instances.

Fleet Size and Mix Split-Delivery Vehicle Routing

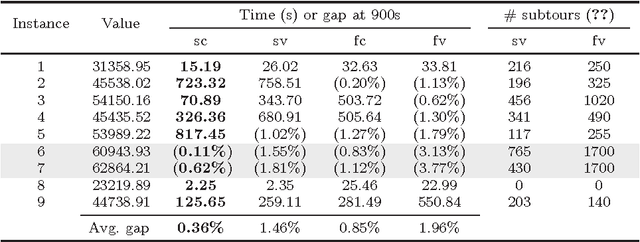
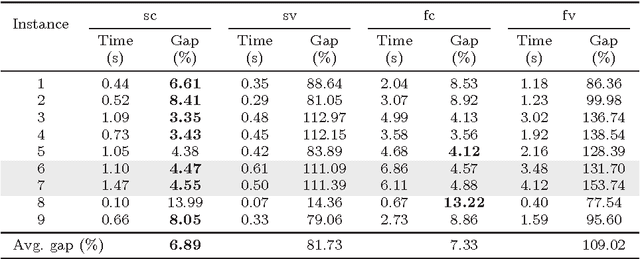
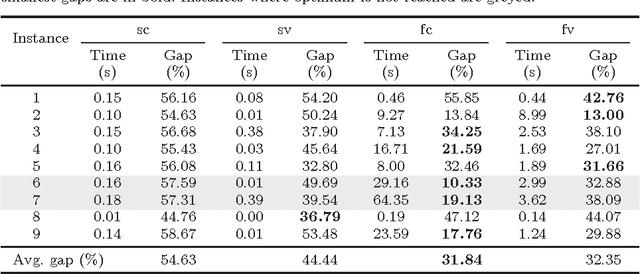
In the classic Vehicle Routing Problem (VRP) a fleet of of vehicles has to visit a set of customers while minimising the operations' costs. We study a rich variant of the VRP featuring split deliveries, an heterogeneous fleet, and vehicle-commodity incompatibility constraints. Our goal is twofold: define the cheapest routing and the most adequate fleet. To do so, we split the problem into two interdependent components: a fleet design component and a routing component. First, we define two Mixed Integer Programming (MIP) formulations for each component. Then we discuss several improvements in the form of valid cuts and symmetry breaking constraints. The main contribution of this paper is a comparison of the four resulting models for this Rich VRP. We highlight their strengths and weaknesses with extensive experiments. Finally, we explore a lightweight integration with Constraint Programming (CP). We use a fast CP model which gives good solutions and use the solution to warm-start our models.

Benders Decomposition for the Design of a Hub and Shuttle Public Transit System

The BusPlus project aims at improving the off-peak hours public transit service in Canberra, Australia. To address the difficulty of covering a large geographic area, BusPlus proposes a hub and shuttle model consisting of a combination of a few high-frequency bus routes between key hubs and a large number of shuttles that bring passengers from their origin to the closest hub and take them from their last bus stop to their destination. This paper focuses on the design of bus network and proposes an efficient solving method to this multimodal network design problem based on the Benders decomposition method. Starting from a MIP formulation of the problem, the paper presents a Benders decomposition approach using dedicated solution techniques for solving independent sub-problems, Pareto optimal cuts, cut bundling, and core point update. Computational results on real-world data from Canberra's public transit system justify the design choices and show that the approach outperforms the MIP formulation by two orders of magnitude. Moreover, the results show that the hub and shuttle model may decrease transit time by a factor of 2, while staying within the costs of the existing transit system.

Symmetry-Based Search Space Reduction For Grid Maps

In this paper we explore a symmetry-based search space reduction technique which can speed up optimal pathfinding on undirected uniform-cost grid maps by up to 38 times. Our technique decomposes grid maps into a set of empty rectangles, removing from each rectangle all interior nodes and possibly some from along the perimeter. We then add a series of macro-edges between selected pairs of remaining perimeter nodes to facilitate provably optimal traversal through each rectangle. We also develop a novel online pruning technique to further speed up search. Our algorithm is fast, memory efficient and retains the same optimality and completeness guarantees as searching on an unmodified grid map.

Informed Heuristics for Guiding Stem-and-Cycle Ejection Chains

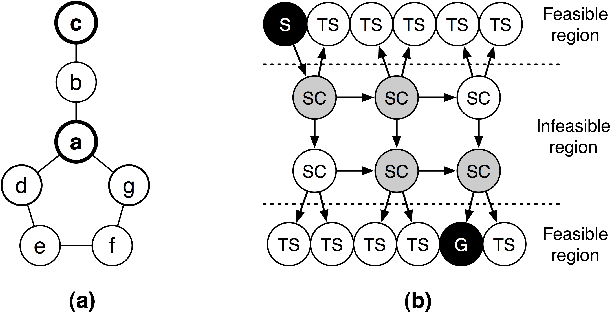
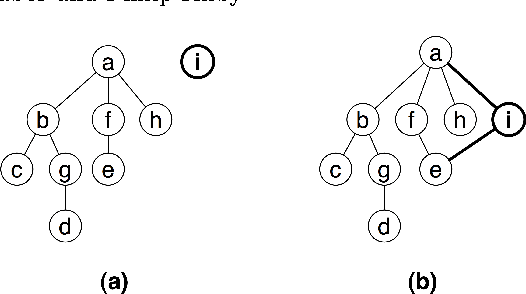
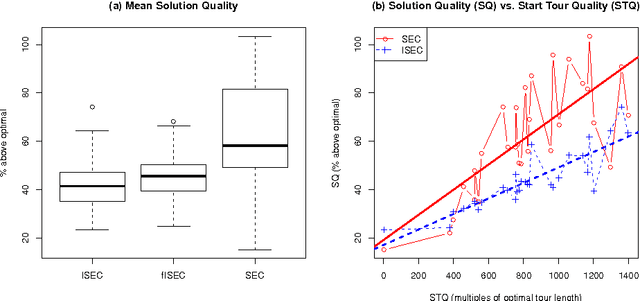
The state of the art in local search for the Traveling Salesman Problem is dominated by ejection chain methods utilising the Stem-and-Cycle reference structure. Though effective such algorithms employ very little information in their successor selection strategy, typically seeking only to minimise the cost of a move. We propose an alternative approach inspired from the AI literature and show how an admissible heuristic can be used to guide successor selection. We undertake an empirical analysis and demonstrate that this technique often produces better results than less informed strategies albeit at the cost of running in higher polynomial time.