Fleet Size and Mix Split-Delivery Vehicle Routing

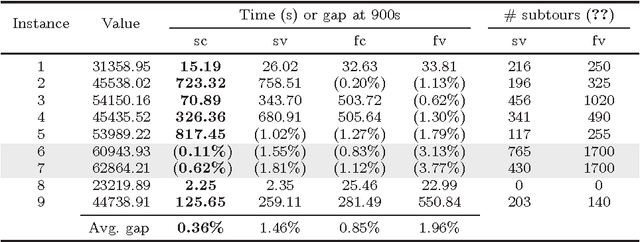
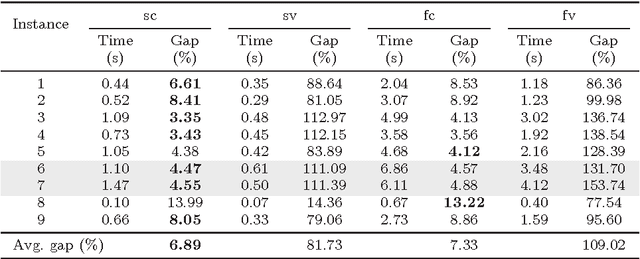
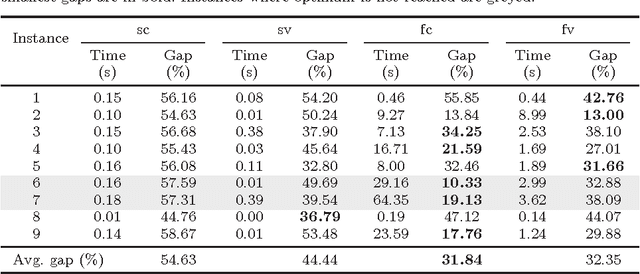
In the classic Vehicle Routing Problem (VRP) a fleet of of vehicles has to visit a set of customers while minimising the operations' costs. We study a rich variant of the VRP featuring split deliveries, an heterogeneous fleet, and vehicle-commodity incompatibility constraints. Our goal is twofold: define the cheapest routing and the most adequate fleet. To do so, we split the problem into two interdependent components: a fleet design component and a routing component. First, we define two Mixed Integer Programming (MIP) formulations for each component. Then we discuss several improvements in the form of valid cuts and symmetry breaking constraints. The main contribution of this paper is a comparison of the four resulting models for this Rich VRP. We highlight their strengths and weaknesses with extensive experiments. Finally, we explore a lightweight integration with Constraint Programming (CP). We use a fast CP model which gives good solutions and use the solution to warm-start our models.

Feature-based tuning of simulated annealing applied to the curriculum-based course timetabling problem

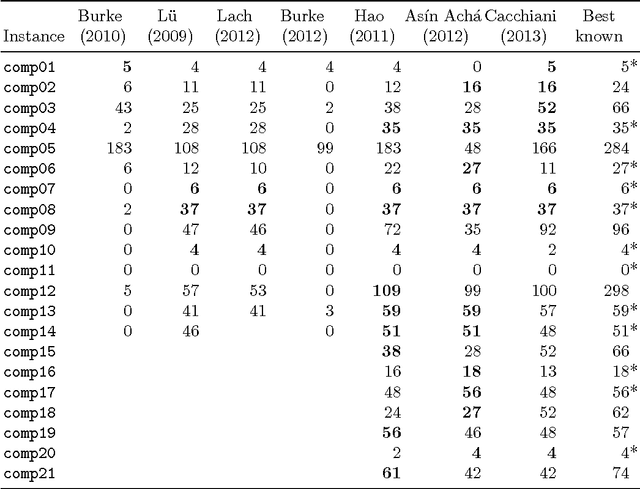
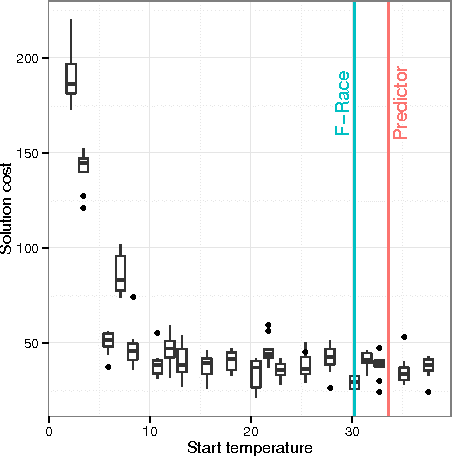
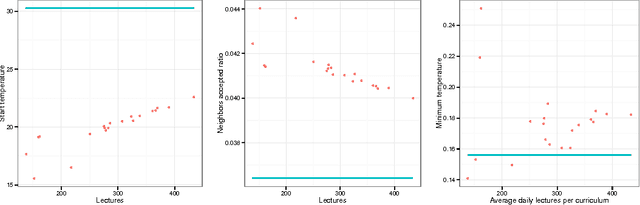
We consider the university course timetabling problem, which is one of the most studied problems in educational timetabling. In particular, we focus our attention on the formulation known as the curriculum-based course timetabling problem, which has been tackled by many researchers and for which there are many available benchmarks. The contribution of this paper is twofold. First, we propose an effective and robust single-stage simulated annealing method for solving the problem. Secondly, we design and apply an extensive and statistically-principled methodology for the parameter tuning procedure. The outcome of this analysis is a methodology for modeling the relationship between search method parameters and instance features that allows us to set the parameters for unseen instances on the basis of a simple inspection of the instance itself. Using this methodology, our algorithm, despite its apparent simplicity, has been able to achieve high quality results on a set of popular benchmarks. A final contribution of the paper is a novel set of real-world instances, which could be used as a benchmark for future comparison.

Balancing bike sharing systems (BBSS): instance generation from the CitiBike NYC data

Bike sharing systems are a very popular means to provide bikes to citizens in a simple and cheap way. The idea is to install bike stations at various points in the city, from which a registered user can easily loan a bike by removing it from a specialized rack. After the ride, the user may return the bike at any station (if there is a free rack). Services of this kind are mainly public or semi-public, often aimed at increasing the attractiveness of non-motorized means of transportation, and are usually free, or almost free, of charge for the users. Depending on their location, bike stations have specific patterns regarding when they are empty or full. For instance, in cities where most jobs are located near the city centre, the commuters cause certain peaks in the morning: the central bike stations are filled, while the stations in the outskirts are emptied. Furthermore, stations located on top of a hill are more likely to be empty, since users are less keen on cycling uphill to return the bike, and often leave their bike at a more reachable station. These issues result in substantial user dissatisfaction which may eventually cause the users to abandon the service. This is why nowadays most bike sharing system providers take measures to rebalance them. Over the last few years, balancing bike sharing systems (BBSS) has become increasingly studied in optimization. As such, generating meaningful instance to serve as a benchmark for the proposed approaches is an important task. In this technical report we describe the procedure we used to generate BBSS problem instances from data of the CitiBike NYC bike sharing system.